What is 3 Phase Supply System?

The three phase supply system having three different windings are placed on the armature at an angular displacement of 120 elect. Each winding has two ends or terminals, so there are six terminals taken out from the three phase alternators. These terminals are connected in different fashions.

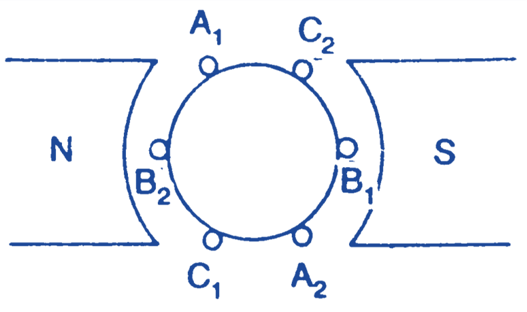
Consider three identical windings, A, B and C winding. A has two ends a₁ and a₂, winding B has two b₁ and b₂, winding C has again two c₁ and c₂. These are placed at 120° apart as shown in Fig. 1 (a). Let these be rotated in the magnetic field produced by a bipolar machine in anticlockwise direction with a speed equal to ω radian/sec.

 

(a)

(b)

Fig. 1. Three Phase generation.

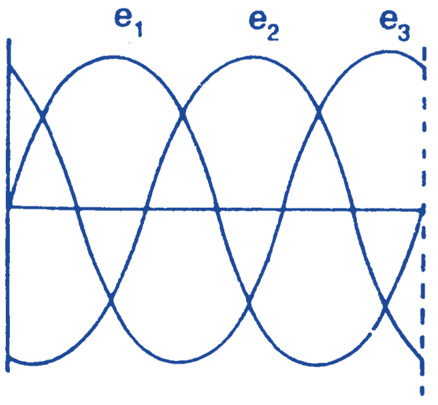
Now depending upon the Fleming’s right hand rule, there will be the production of the voltage displaced at 120° elect. apart. This e.m.f.s. are same in magnitude and frequency. These are illustrated by a sine wave as shown in Fig. 1 (b). I.et A is at 0° elect. then the e.m.f. e₁ will start from zero degree, phase B from 120° apart will have a sine wave as e₂ and phase C, 240° elect. apart is shown by e₃. E.m.f. e₂ initially is negative and approaching to negative maximum value. The e.m.f. e₃ is in positive direction and decreasing to zero value as shown. These e.m.f.s. can be said as

e₁ = E_m sin ωt

e₂ = E_m sin (ωt – 120)

e₃ = E_m sin (ωt – 240)

Similarly the current can be drawn keeping in mind the angle of lag or lead.

INTER CONNECTIONS OF THREE PHASES

There are the following different ways of connecting these three windings for obtaining three phase supply for the load.

1. Three phase six wire system.
2. Delta connection or Mesh connections
3. Star connection or Wye connection

Three phase six wire system

In this case the load is divided into three equal circuit and every load circuit is connected across individual circuits; as shown in Fig. 3.

Fig. 2: Three Phase Windings

Let E_p1, E_p2 and E_p3 be the phase voltages and I_p1, I_p2 and I_p3 be the currents respectively. so the power in different phase are:

Phase A = E_p1 I_p1 cos Φ      Watts

Phase B = E_p2 I_p2 cos Φ      Watts

Phase C = E_p3 I_p3 cos Φ     Watts

In a particular machine when phase windings are identical so it will have the characteristics as given.

1. The voltage across each phase is same because the windings are identical.
2. In case when load is equal, the same current will flow through each phase.

The total power will now be equal to
= 3 × Phase power
= 3 × E_p I_p cos Φ.
In case of unbalanced loads, the currents i.e. I_p1, I_p2 and I_p3 are different and total power will be the sum of individual phase powers. This system is not adopted nowadays.