In this topic, you study How to derive an expression for Peak to Peak Ripple voltage of the capacitor for Buck Regulator.
The buck regulator produces a lower average output voltage than the dc source input voltage. Let us assume large filter capacitance C connected across the load so that output voltage remains almost constant. The Resistive load is considered.
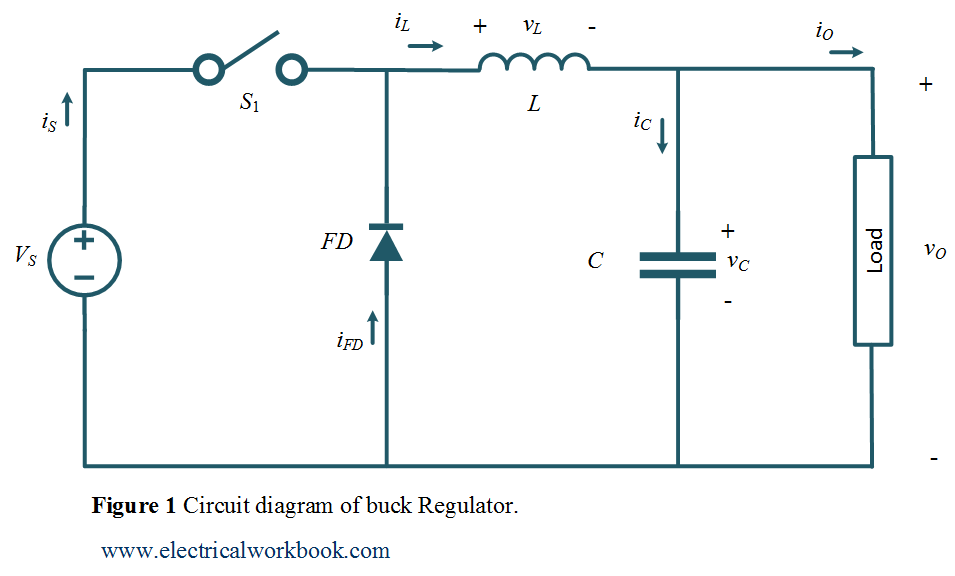
Circuit diagram
The working of a buck regulator is explained using the circuit diagram as shown in Figure 1. The switch ${S_1}$ shown in the circuit diagram can be a conventional thyristor i.e., SCR, a GTO thyristor, a power transistor, or a MOSFET.
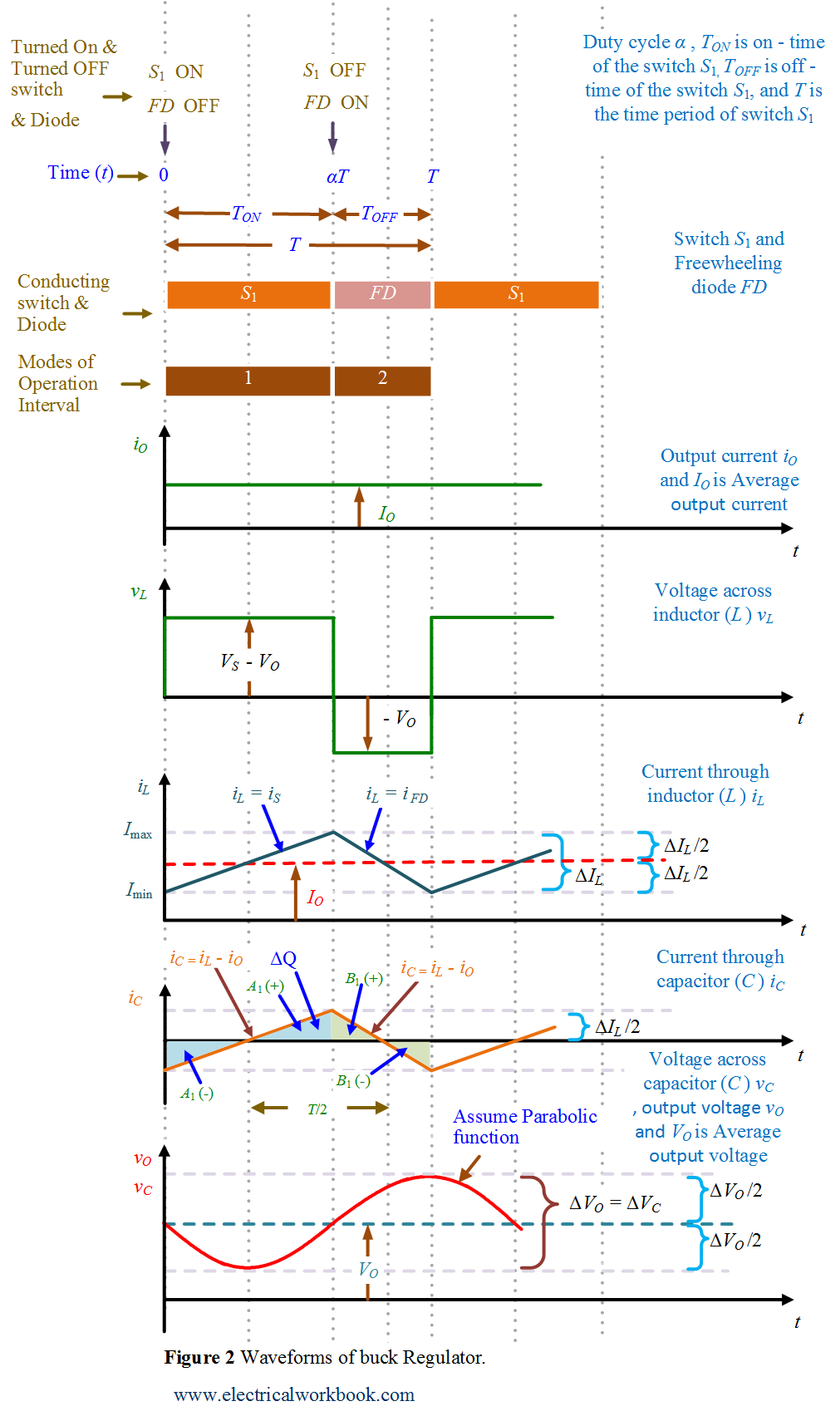
Waveforms
The typical waveforms in the converter are shown in Figure 2.
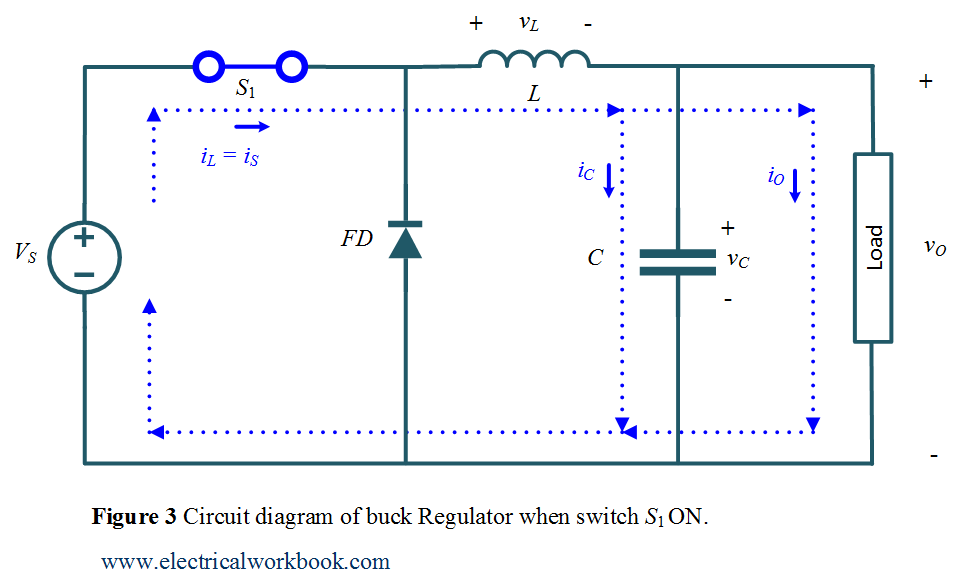
Mode of Operation Interval 1: –
The time interval is 0 ≤ t ≤ ${T_{ON}}$. The switch ${S_1}$ is turned on. The circuit diagram for Mode of Operation Interval 1 is shown in Figure 3 and the corresponding waveforms are shown in Figure 2.
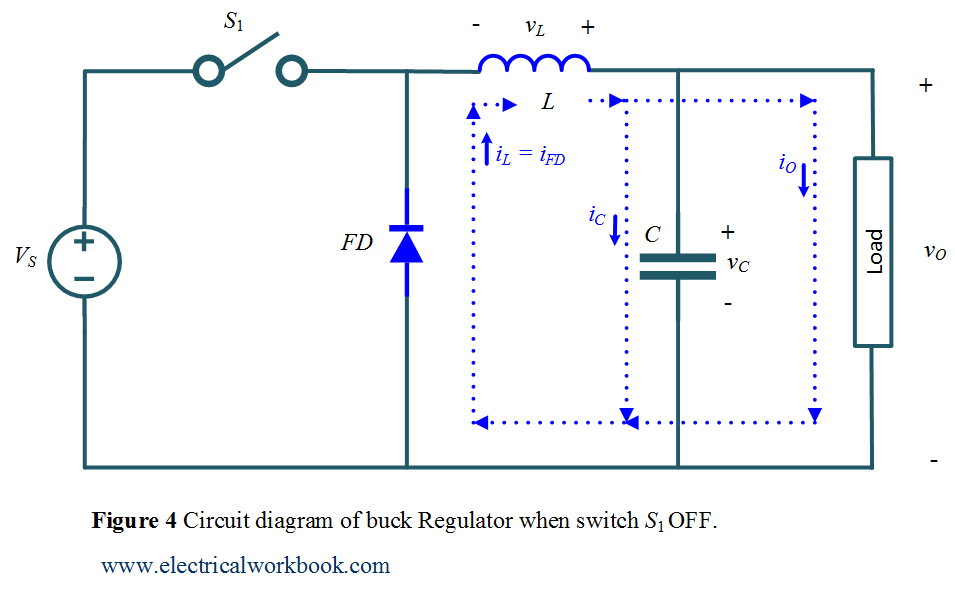
Mode of Operation Interval 2: –
The time interval is ${T_{ON}}$ ≤ t ≤ ${T_{OFF}}$. The circuit diagram for Mode of Operation Interval 2 is shown in Figure 4 and the corresponding waveforms are shown in Figure 2.
As shown in Figure 2, the area of each of the triangles representing charge $\Delta Q$ in the waveform of capacitor current so area of triangle ${A_1}$( + ) write as
\[\Delta Q = \frac{1}{2}.\frac{T}{2}.\frac{{\Delta {I_L}}}{2}….(1)\]
The incremental voltage $\Delta {V_O}$ across the capacitor is associated with incremental charge $\Delta Q$ by the relation
\[\Delta {V_O} = \Delta {V_C} = \frac{{\Delta Q}}{C}….(2)\]
Using Equation 1 and Equation 2 gives
\[\Delta {V_O} = \Delta {V_C} = \frac{{\Delta {I_L}}}{{8fC}}…..(3)\]
The peak to peak ripple current of inductor is given as
\[\Delta {I_L} = \frac{{{V_S}(1 – \alpha )}}{L}.\frac{\alpha }{f}…(4)\]
Using Equation 3 and Equation 4 gives
\[\Delta {V_O} = \frac{{\alpha (1 – \alpha ){V_S}}}{{8\hspace{0.1cm}{f^2}\hspace{0.1cm}CL}}….(5)\]
Equation 5 describes the Peak to Peak Ripple Voltage of Capacitor in buck converter.