In this topic, you study Efficiency of DC Motor.
The efficiency of a dc motor is defined as the ratio of power output to power input and can be expressed as
\[\text{ }\!\!\eta\!\!\text{ }=\text{ }\frac{\text{Power output}}{\text{Power intput}}=\frac{\text{Power output}}{\text{Power output}+\text{Losses}}\]
\[=\frac{\text{Power Input – Losses}}{\text{Power Input}}\]
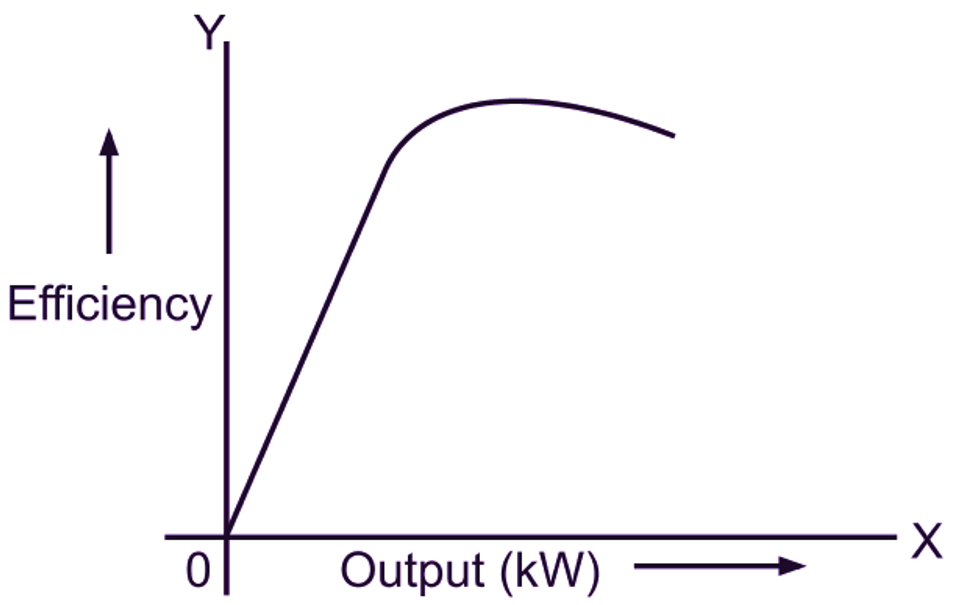
Fig. 1: Efficiency curve for a dc motor
Efficiency is generally expressed as a percentage. The efficiency of a dc motor depends on the power output. Initially with low power outputs, efficiency is poor due to the constant losses. As the output increases, the efficiency increases till it reaches a certain maximum value. If the output is still further increased, then the efficiency decreases due to the rapid rise in the variable losses. The motors are normally designed to have maximum efficiency while working at or near full load. The efficiency of a dc motor at normal operating conditions may be as high as 95%. A typical efficiency curve showing the manner in which the efficiency varies with the output is shown in Fig. 1.
CONDITION FOR MAXIMUM EFFICIENCY
Condition for maximum efficiency of a dc motor can be derived by using the expression for its efficiency.
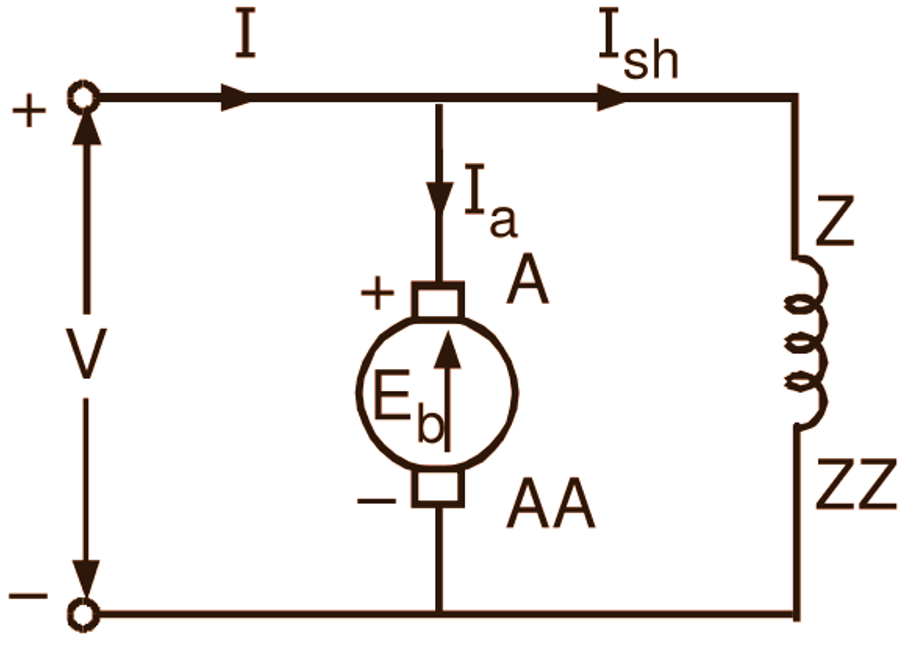
Fig. 2: DC shunt motor
Considering the case of a dc shunt motor (Fig. 2) and using usual notations, we have,
\[\text{Power Input}=\text{VI}\]
\[\text{Losses}=\text{I}_{\text{a}}^{\text{2}}{{\text{R}}_{\text{a}}}\text{+}{{\text{P}}_{\text{c}}}\]
where Pc represents constant losses namely, iron losses, field copper loss and mechanical
\[\text{Power output}=\text{VI}-\text{I}_{\text{a}}^{\text{2}}{{\text{R}}_{\text{a}}}-{{\text{P}}_{\text{c}}}\]
\[\eta =\frac{\text{Power output}}{\text{Power intput}}\]
\[=\frac{\text{Power Input – Losses}}{\text{Power Input}}\]
\[=\frac{\text{VI}-\text{I}_{\text{a}}^{\text{2}}{{\text{R}}_{\text{a}}}-{{\text{P}}_{\text{c}}}}{\text{VI}}\]
Now, for a dc shunt motor, field current (Ish) being usually very small as compared to the motor current (I),
\[{{\text{I}}_{\text{a}}}=\text{I}-{{\text{I}}_{\text{sh}}}\approx \text{I}\]
\[\eta =\frac{\text{VI}-{{\text{I}}^{2}}{{\text{R}}_{\text{a}}}-{{\text{P}}_{\text{c}}}}{\text{VI}}\]
\[=1-\frac{\text{I}{{\text{R}}_{\text{a}}}}{\text{V}}-\frac{{{\text{P}}_{\text{c}}}}{\text{VI}}\]
For efficiency of a dc motor to be maximum,
\[\frac{\text{d }\!\!\eta\!\!\text{ }}{\text{dI}}=-\frac{{{\text{R}}_{\text{a}}}}{\text{V}}-\frac{{{\text{P}}_{\text{c}}}}{\text{V}{{\text{I}}^{2}}}=0\]
\[{{\text{I}}^{2}}{{\text{R}}_{\text{a}}}=\text{I}_{\text{a}}^{\text{2}}{{\text{R}}_{\text{a}}}={{\text{P}}_{\text{c}}}\]
Thus, efficiency of the dc motor is maximum when the variable loss (i.e. copper loss) is equal to the constant loss.
Example 1: A 250 V dc. shunt motor takes a current of 4 A from 250 V mains when running at no load. The resistance of the armature circuit is 1 Ω and that of the field circuit is 250 Ω. Calculate (a) the efficiency of the motor when it draws a current of 20 A from the mains, (b) The armature current for which the efficiency is a maximum, (c) The value of maximum efficiency.
