In this topic, you study the Energy and Power Signals theory, properties & solved examples.
Energy and Power Signals
Let us consider a circuit having resitance R supplied by a ac source voltage $v(t)$ as shown in Figure 1 is
$v(t) = {V_m}\sin \omega t$
The current passes throgh resistance R will be
\[i(t) = \frac{{v(t)}}{R}\]
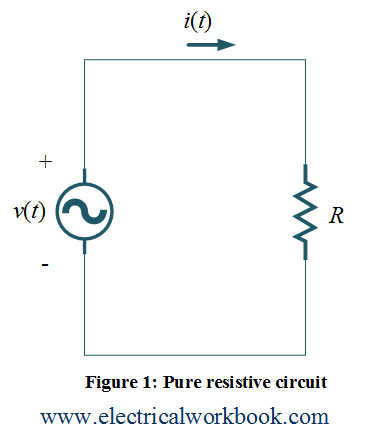
The instantaneous power $p(t)$ is defined by the product of instantaneous voltage $v(t)$ and instantaneous current $i(t)$.
$p(t) = v(t)i(t)$
\[p(t) = v(t)i(t) = \frac{{{v^2}(t)}}{R}\]
or,
$p(t) = {i^2}(t)R$
or, normalized power
$p(t) = {v^2}(t){\text{ or }}{i^2}(t)$
Equivalently $ p(t) $ can be expressed as $p(t) = {x^2}(t)$, where $x(t)$ is continuous-time signal [like $v(t)$ or $i(t)$]. Since the average power $P$ is related to energy $E$ as
\[P = \frac{{dE}}{{dt}}\]
For an arbitrary continuous-time signal $x(t)$, the total energy $E$ of $x(t)$ is defined as
\[E = \mathop {\lim }\limits_{T \to \infty } \int\limits_{ – T/2}^{ + T/2} {{x^2}(t)} dt\]
or, equvalently
\[E = \int\limits_{ – \infty }^{ + \infty } {|x(t){|^2}} dt\]
For an arbitrary continuous-time signal $x(t)$, the average power $P$ of $x(t)$ is defined as
In case of Non-periodic signal
\[P = \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int\limits_{ – T/2}^{ + T/2} {|x(t){|^2}} dt\]
In case of Periodic signal
\[P = \frac{1}{T}\int\limits_{ – T/2}^{ + T/2} {|x(t){|^2}} dt\]
Note: Based on definitions, the following points of Energy and power signals are defined as
- A signal $x(t)$ referred to be an energy signal if and only if the total energy $E$ is finite i.e. 0 < $E$ < $\infty $, and so average power $P$ = 0.
- A signal $x(t)$ referred to be power signal if and only if 0 < $P$ < $\infty $, and so energy $E$ = $\infty $.
- A signal $x(t)$ referred to be neither energy nor power signal if both energy and power are equal to infinity.
Example 1: Calculate the power of signal $x(t)$ shown in Figure 2.
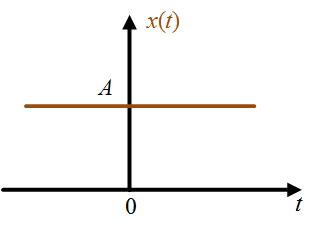
Figure 2
Solution 1: The signal $x(t)$ is Non-periodic so by definition
\[P = \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int\limits_{ – T/2}^{ + T/2} {|x(t){|^2}} dt\]
From Figure 2, $x(t)$ = A, for all $t$ and hence,
\[P = \frac{1}{T}\int\limits_{ – T/2}^{ + T/2} {|A{|^2}} dt = {A^2}\]
Example 2: Calculate the energy of signal $x(t)$ shown in Figure 3.
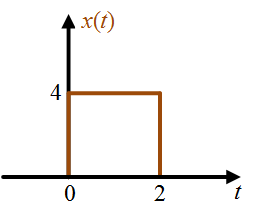
Figure 3
Solution 2: By definition
\[E = \int\limits_{ – \infty }^{ + \infty } {|x(t){|^2}} dt\]
From Figure 3, $x(t)$ = 4, for the time 0 ≤ $t$ ≤ 2 and hence,
\[E = \int\limits_0^2 {{4^2}} dt = {4^2} \times 2 = 32\]