In this topic, you study the Even and odd signals theory, properties & solved examples.
Even Signals
A continuous-time signal $x(t)$ is is said to be even signal if
$x(t)=x(-t)$
for all $t$. Figure 1 shows an even signal and it follows that
- Even signals are symmetrical or mirror image about the $y$ – axis of the $ x – y $ plane.
- The value at time $t$ is the same as at time $-t$.
- The area under the even signal is two times its one side area.
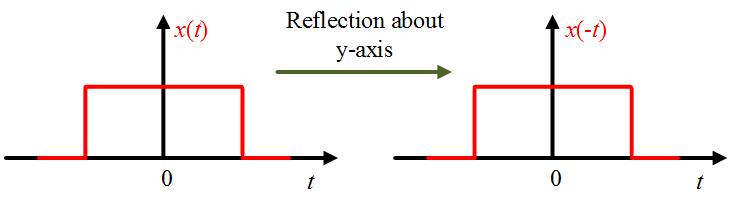
Figure 1: Even signal.
Odd Signals
A continuous-time signal $x(t)$ is is said to be an odd signal if
$x(t)=-x(-t)$
for all $t$. Figure 2 shows an odd signal and it follows that
- Odd signals are Antisymmetric about the origin.
- The value at time $t$ is negative of its value at time $-t$ for all $t$.
- The area under the odd signal is zero.
- The odd signal must be zero at $t$ = 0 so that $x(0) = -x(0)$.
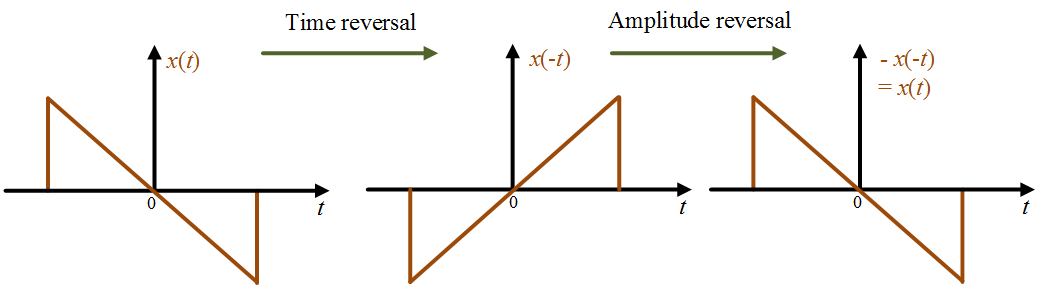
Figure 2: Odd signal.
Example 1: Check whether the following signals are even, odd or neither even nor odd.
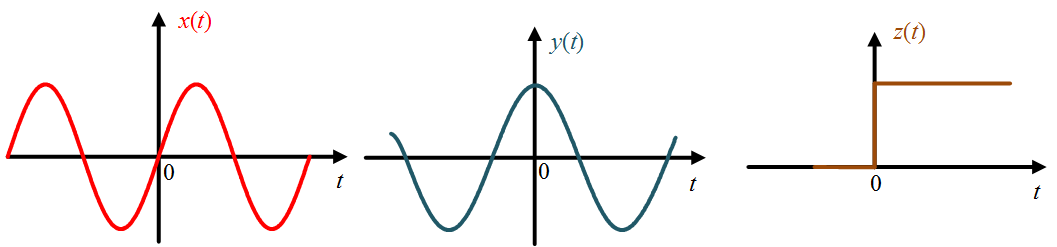
Figure 3
Solution 1: with refrence to Figure 3, for signal $x(t)$, $x(t) = -x(-t)$ so $x(t)$ is the odd signal. For signal $y(t)$, $y(t) = y(-t)$ so $y(t)$ is the even signal. The signal $z(t)$ does not follow the condition of even and odd signals so it is neither even nor odd signal.