In this topic, you study the Invertible and Non Invertible Systems theory, definition & solved examples.
Let $x(t)$ and $y(t)$ be the input and output signals, respectively, of a system shown in Figure 1. Then the transformation of $x(t)$ into $y(t)$ is represented by the mathematical notation
$y(t) = {\mathbf{T}}x(t)$
where $\mathbf{T}$ is the operator which defined rule by which $x(t)$ is transformed into $y(t)$.
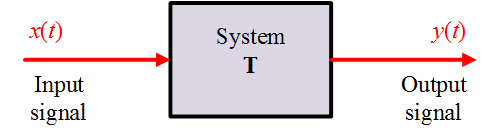
Figure 1: System with a single input and output signal.
Invertible System
A system is called invertible if there should be one to one mapping between input and output at a particular instant and when an invertible system cascaded with its inverse system then gain of will be equal to one. In other words, if the input can be recovered from the system output, the system is said to be invertible, it is shown in Figure 2. Mathematically the $y(t)$ signal write as
\[y(t) = {\mathbf{T}}x(t)\]
And the $z(t)$ signal write as
\[z(t) = {{\mathbf{T}}^{ – 1}}y(t)\]
\[ = {{\mathbf{T}}^{ – 1}}{\mathbf{T}}x(t)\]
\[ = x(t)\]
Thus
\[z(t)= x(t)\]

Figure 2: Invertible System.
Non Invertible System
A system is called non-invertible if there should be many to one mapping between input and output at a particular instant.
Example : Determine whether or not each of the following systems are invertible with input $x(t)$ and output $y(t)$.
(i) \[y(t) = 10 + x(t)\]
(ii) \[y(t) = {x^2}(t)\]\]
Solution : (i) \[y(t) = 10 + x(t)\]
Let, $x(t) = 2$ which is the dc signal input so,
\[y(t) = 10 + 2 = 12\]
Let, $x(t) = 21$ which is the dc signal input so,
\[y(t) = 10 + 21 = 31\]
Since different inputs leads to different output hence system is invertible.
Solution : (ii) \[y(t) = {x^2}(t)\]
Let, $x(t) = 5$ which is the dc signal input so,
\[y(t) = 5^2 = 25\]
Let, $x(t) = -5$ which is the dc signal input so,
\[y(t) = (-5)^2 = 25\]
Since different inputs leads to same output hence system is non-invertible.