The e.m.f. is induced in a circuit if it links with the changing flux produced by the other neighbouring coil. This e.m.f. is known as mutually induced e.m.f. and the phenomenon is known as mutual induction.
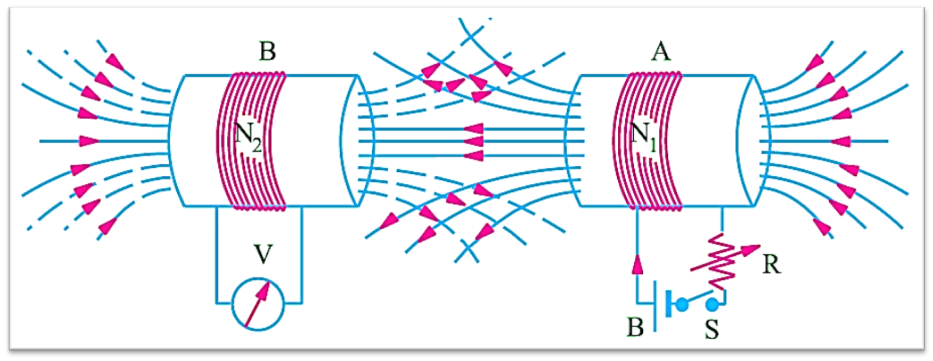
Fig. 1. Mutual induction.
The figure shows two coils A and B placed side by side. A galvanometer is connected across the coil B and coil A is connected to a battery through an ammeter and variable resistance to vary the current. When the switch is on, the current changes producing a changing magnetic field which links the coil B and according to the Faradays laws of electromagnetic induction the e.m.f. is induced in coil B. The induction of voltage will last only as long as the change of flux is there. This e.m.f. is known as mutually induced e.m.f. and the phenomenon of induction as the mutual induction.
Uses. This principle is used in two winding transformers on a.c. where the direction and magnitude of the current always keeps on changing.
Coefficient of mutual induction (M)
It is denoted by the letter M. If there are two coils having N1 and N2 number of turns; than the coefficient of mutual inductance between the two coils is defined as the weber-turns in one coil due to one ampere current in the other neighbouring coil.
Let there be I, ampere current flowing in one coil produces Φ1 Wb. flux. Now this flux links with the second coil without loss of any flux. Now the flux linkage (Weber turns) in the second coil for unit current in the first coil are
\[=\frac{{{N}_{2}}\cdot {{\phi }_{1}}}{{{I}_{1}}}\]
Now by definition, we can say that
\[M=\frac{{{N}_{2}}{{\phi }_{1}}}{{{I}_{1}}}\]
if N1Φ1 = 1 and I = 1 A in that case M = l, which can be defined as the two coils are said to have a mutual inductance of 1 H if one ampere current when flowing in one coil produces a flux linkage of one Wb-tum in the other neighbouring coil.
It can otherwise be defined as two coils will have a mutual inductance of one henry if a current changing at the rate of one ampere per second in one coil induces an e.m.f. of one volt in the other coil.
Coefficient of coupling
L1 = Coefficient of self inductance of coil 1
L2 = Coefficient of self inductance of second coil.
M = Coefficient of mutual inductance,
Then
\[M=K\sqrt{{{L}_{1}}{{L}_{2}}}\]
or
\[K=\frac{M}{\sqrt{{{L}_{1}}{{L}_{2}}}}\]
When the two coils are tightly coupled i.e. the flux produced by coil links with the other coil completely the K, coupling coefficient is unity. If the flux produced by one coil does not link the other coil than the value of coefficient of coupling is zero i.e. the coils are magnetically isolated from each other.