In this topic, you study the Periodic and Aperiodic Signals theory & solved examples.
Periodic Signals
A continuous-time signal $x(t)$ is called periodic if
$x(t+T)=x(t)$
for all $t$ and the time period $T$ of the signal $x(t)$ is non zero positive value. Figure 1 shows a periodic signal and it follows that
$x(t+mT)=x(t)$
$m$ is an integer for all $t$. 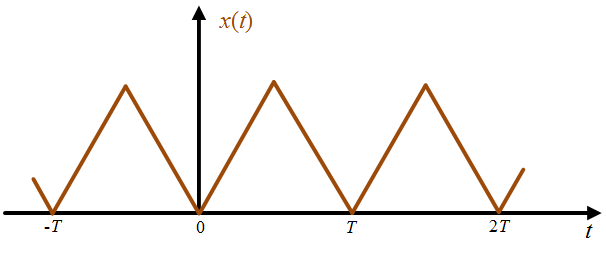
Figure 1: Periodic signal
The fundamental time period $T_0$ of $x(t)$ is the smallest and positive value of $T$ for which signal is periodic. We can conclude that a periodic signal is one which
- Repeats over and over
- Contains all the time ($ – \infty {\text{ to + }}\infty $)
Example 1: For a periodic signal $x(t)$ shown in Figure 2, find the fundamental time period.
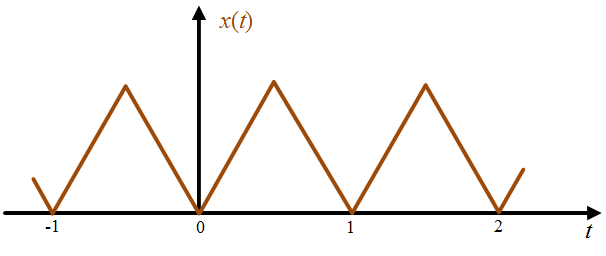
Figure 2
Solution 1: with refrence to Figure 2
$ x(t+ T_0) = x(t+1) = x(t) $
so fundamental time period $T_0$ is 1.
Aperiodic Signals
Any continuous-time signal which is not periodic is called a nonperiodic (or aperiodic) signal.
Example 2: Check whether the signal $x(t)$ shown in Figure 3 is periodic or not.
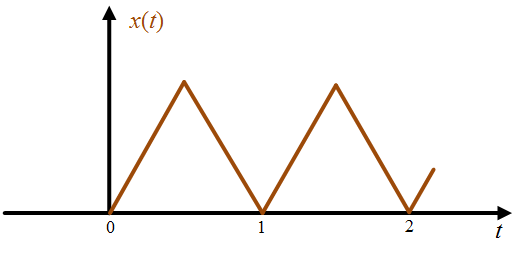
Figure 3
Solution 2: with refrence to Figure 3, the signal $x(t)$ contains the time $ 0 {\text{ to + }}\infty $, so
$ x(-t) = 0 $
Hence the signal $x(t)$ is aperiodic.