In this topic, you study the Time Variant & Time-Invariant Systems theory, definition & solved examples.
Let $x(t)$ and $y(t)$ be the input and output signals, respectively, of a system shown in Figure 1. Then the transformation of $x(t)$ into $y(t)$ is represented by the mathematical notation
$y(t) = {\mathbf{T}}x(t)$
where $\mathbf{T}$ is the operator which defined rule by which $x(t)$ is transformed into $y(t)$.
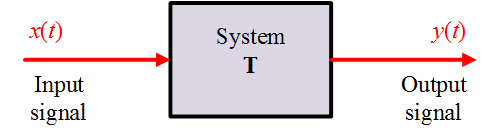
Figure 1: System with a single input and output signal.
A system is called time-invariant if a time shift in the input signal $x(t – {t_0})$ causes the same time shift in the output signal $y(t – {t_0})$, it is shown in Figure 2.
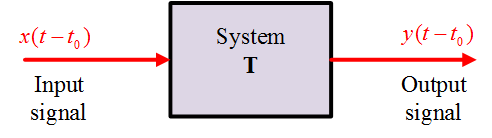
Figure 2: Time-Invariant System.
Example : Determine whether or not each of the following systems are time variant with input $x(t)$ and output $y(t)$.
(i) \[y(t) = tx(t)\]
(ii) \[y(t) = \cos t \cdot x(t)\]
(iii) \[y(t) = 2 + x(t)\]
Solution : (i) \[y(t) = tx(t)\]
delay input by $t_0$, let the output be ${y_1}(t)$
\[{y_1}(t) = tx(t – {t_0})\]
delay output by $t_0$, let the output be ${y_2}(t)$
\[{y_2}(t) = y(t – {t_0}) = (t – {t_0})x(t – {t_0})\]
\[{y_1}(t) \ne {y_2}(t)\]
hence the system is time variant.
Solution : (ii) \[y(t) = \cos t \cdot x(t)\]
delay input by $t_0$, let the output be ${y_1}(t)$
\[{y_1}(t) = \cos t \cdot x(t – {t_0})\]
delay output by $t_0$, let the output be ${y_2}(t)$
\[{y_2}(t) = y(t – {t_0}) = \cos (t – {t_0})x(t – {t_0})\]
\[{y_1}(t) \ne {y_2}(t)\]
hence the system is time variant.
Solution : (iii) \[y(t) = 2 + x(t)\]
delay input by $t_0$, let the output be ${y_1}(t)$
\[{y_1}(t) = 2 + x(t – {t_0})\]
delay output by $t_0$, let the output be ${y_2}(t)$
\[{y_2}(t) = y(t – {t_0}) = 2 + x(t – {t_0})\]
\[{y_1}(t) = {y_2}(t)\]
hence the system is time-invariant.