In this topic, you study Back EMF in DC Motor.
When the current carrying conductors of the armature winding are placed in the magnetic field produced by the field winding, each of them experiences a force and as a result, the armature of the motor starts rotating. When these armature conductors start rotating, the flux which is responsible for their rotation is cut and consequently an emf is induced in them in accordance with Faraday’s law of electromagnetic induction. This emf always acts in opposition with the applied voltage (V) as per Lenz’s law and therefore it is known as back emf (Eb) or counter e.m.f: (Fig. 1). Since the counter emf opposes the applied voltage across the armature, the net voltage acting in the armature circuit is the difference between the two (i.e. V – Eb).
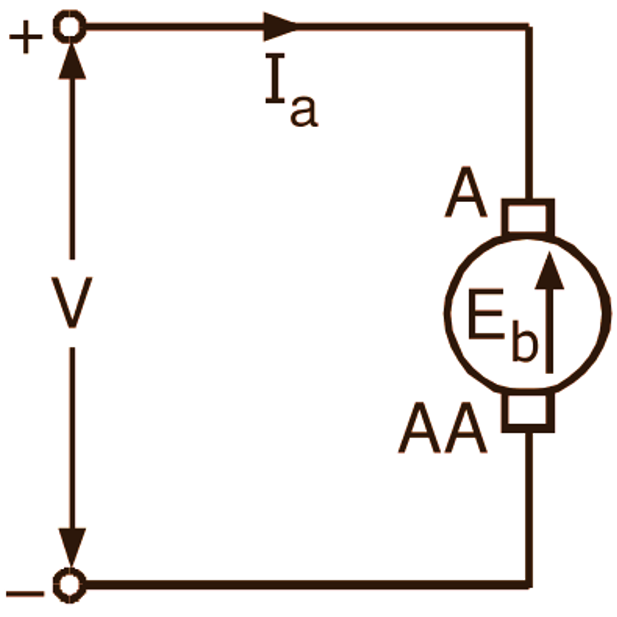
Fig. 1: Back emf or counter emf in the armature of a dc motor
It is this effective voltage which determines the value of the armature current (Ia). If Ra is the armature resistance, then from Ohm’s law,
\[{{\text{I}}_{\text{a}}}=\frac{\text{V}-{{\text{E}}_{\text{b}}}}{{{\text{R}}_{\text{a}}}}\text{ amperes}….(1)\]
In the running condition, Eb is nearly equal to V. The internal resistance of the armature of a dc motor being very low, it is the back emf which mainly limits the armature current in the running condition of the motor. The Equation (1) can be rewritten as
\[\text{V}={{\text{E}}_{\text{b}}}+{{\text{I}}_{\text{a}}}{{\text{R}}_{\text{a}}}\]
This is known as voltage equation of the motor. It shows that in order to maintain the current supply to armature, the applied voltage has to overcome not only the resistance of the armature winding but also the back emf. Similar to generator, the magnitude of the back emf generated in the armature of a dc motor is given by the following expression :
\[{{\text{E}}_{\text{b}}}=\frac{\text{Z}\phi \text{N}}{60}.\frac{\text{P}}{\text{A}}\]
where,
Φ = Flux per pole, in webers
N = Speed, in revolutions per minute
Z = Number of armature conductors
P = Number of poles
A = Number of parallel paths
Example 1: A 230 V, 4 pole dc motor has an armature circuit resistance of 0.5 Ω. Find the back e.m.f: in the motor when The armature current is 25 A. If The armature winding is lap connected with 320 conductors and the useful flux per pole is 50 mWb, calculate the speed.
