This Block rotor test of Induction motor test is analogues to the short circuit test on transformer. This test gives information about copper loss of motor. The circuit diagram for this test is shown in Fig. 1.
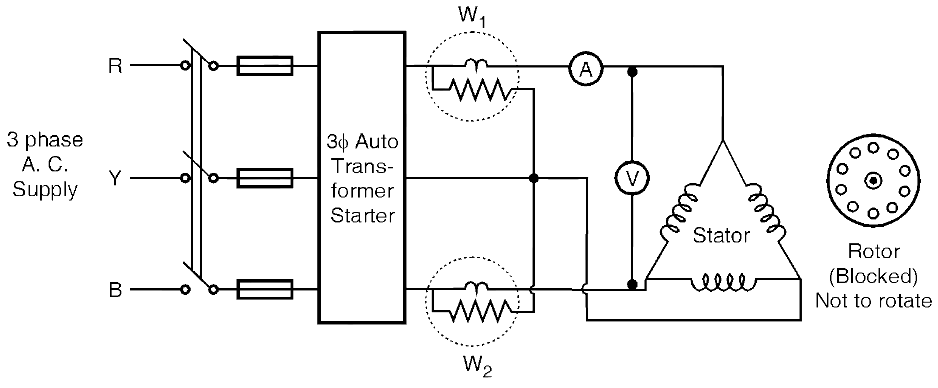
Fig. 1: Blocked rotor test of Induction motor
The rotor is held stationary or rotor is blocked i.e. it is not allowed to rotate. The stator supply voltage is gradually increased till motor carries rated or full load current. The corresponding readings are noted down. The voltage required to circulate rated current is very less (merely 5 to 8% of rated value) so main flux is considerably less because flux is proportional to voltage. Hence the iron loss occurring is very less and can be neglected safely. The stator and hence rotor carries rated current so copper loss occurs. Since no useful output is extracted from motor (rotor is blocked), the entire power input is equal to copper losses. So wattmeter reading represents copper losses.
Observation Table of Blocked Rotor Test
| Vsc
(Volt) |
Isc
(Amp) |
W1 (Watt) |
W2
(Watt) |
Wsc = W1 + W2 |
Vsc = Voltage required to circulate rated current at short circuit condition/ blocked rotor condition
Isc = rated current at short circuiting condition
Wsc = Copper loss at full load
Calculations of Blocked Rotor Test
Wsc = total copper loss
\[{{W}_{SC}}=3I_{SC}^{2}{{R}_{01}}\]
Where R01 is equivalent resistance of motor referred to stator or primary side
From which
\[{{R}_{01}}=\frac{{{W}_{SC}}}{3I_{SC}^{2}}\]
Equivalent impedance,
\[{{Z}_{01}}=\frac{{{V}_{SC}}}{{{I}_{SC}}}\]
\[{{Z}_{01}}=\sqrt{R_{01}^{2}+X_{01}^{2}}\]
\[{{X}_{01}}=\sqrt{Z_{01}^{2}+R_{01}^{2}}\]
Thus parameters of equivalent circuit referred to stator side are calculated.
Using no load an blocked rotor test efficiency of motor can be calculated as follows
\[\eta =\frac{\text{Output}}{\text{Output + Iron loss + Copper loss}}\times 100\]
\[\eta =\frac{\text{Output}}{\text{Output + }{{\text{W}}_{0}}\text{ + }{{\text{W}}_{\text{SC}}}}\times 100\]
