The differences between a refrigerator and a heat pump are as follows,
| Refrigerator | Heat pump |
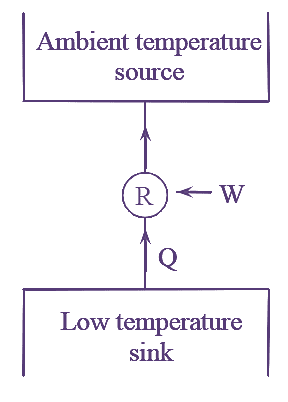
| 1. Refrigerator may be defined as a machine, which is used for cooling the system.
2. A simple cyclic process of this machine is given as,
3. In a refrigerator, an engine can be used to absorb heat at low temperature sink and reject it to ambient temperature source as shown in the figure. 4. The main objective of this machine is to refrigerate a body at low temperature. |
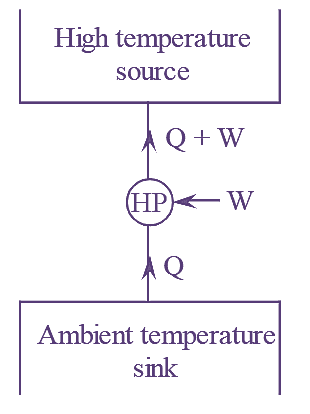
1. Heat pump may be defined as a machine or pump, which is used for heating the system.
2. A simple cyclic process of this machine is given as,
3. In heat pump, heat is absorbed at ambient temperature sink and rejected to the high temperature source as shown in figure. 4. The main objective of this machine is to reject energy as heat to high temperature. |
Performance Factor (or) Coefficient of Performance of Heat Pump
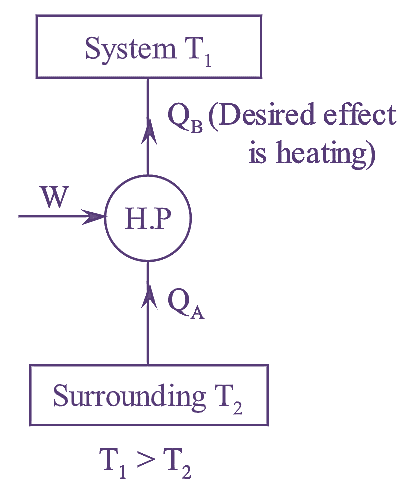
Figure : Heat Pump
Coefficient of Performance (C.O.P) is used to express the performance of the heat pump. It is defined as the ratio of heat supplied by the heat pump from the surrounding to the system at higher temperature to the net work supplied to run the heat pump. Mathematically it is written as.
\[\text{C}\text{.O}\text{.P}=\frac{\text{Heat supplied by heat pump to the system}}{\text{Net work supplied to heat pump}}\]
Applying first law of thermodynamics,
Workdone,
\[W={{Q}_{B}}-{{Q}_{A}}\]
\[{{\left( \text{C}\text{.O}\text{.P} \right)}_{Heat\text{ }pump}}\text{=}\frac{Desired\text{ }effect}{Work\text{ }done}=\frac{{{Q}_{B}}}{{{Q}_{B}}-{{Q}_{A}}}\]
\[{{\left( \text{C}\text{.O}\text{.P} \right)}_{Heat\text{ }pump}}=\frac{{{Q}_{B}}}{{{Q}_{B}}-{{Q}_{A}}}\]
Performance Factor (or) Coefficient of Performance of Refrigerator
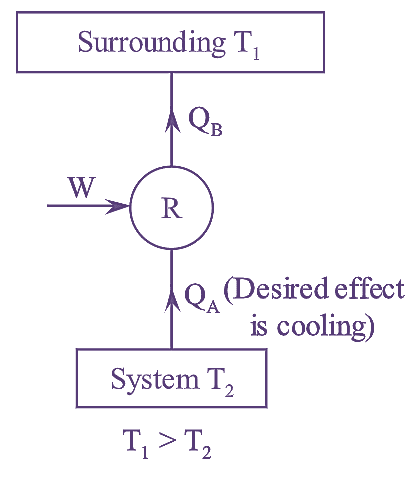
Figure : Refrigerator
It is defined as the ratio of heat extracted from the surroundings to be cooled to the net work supplied.
Applying first law of thermodynamics,
Workdone,
\[W={{Q}_{B}}-{{Q}_{A}}\]
Then,
\[{{\left( \text{C}\text{.O}\text{.P} \right)}_{refrigerator}}\text{=}\frac{Desired\text{ }effect}{Work\text{ }done}\]
\[=\frac{{{Q}_{A}}}{W}=\frac{{{Q}_{B}}}{{{Q}_{B}}-{{Q}_{A}}}\]