In this topic, you study Efficiency of a Transformer.
The efficiency of a transformer is defined as the ratio of output power to input power. It is denoted by,
\[\text{Efficiency }\!\!~\!\!\text{ }\text{ }\eta \text{ }\!\!~\!\!\text{ }=\text{ }\frac{\text{Output power}}{\text{Input power}}\]
\[=\frac{\text{Output power}}{\text{Output power + Losses}}\]
Since the output power is always less than the input power due to losses in the transformer, the efficiency of the practical transformer is always between 0 and 1 i.e. 0% and 100
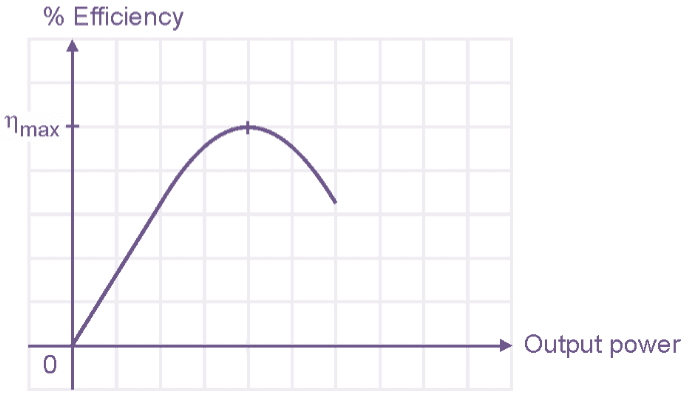
Figure 1: Output power versus Efficiency of a Transformer
The efficiency of an ideal transformer be equal to 1 or 100% because the losses in the ideal transformer be zero. The graph of output power versus efficiency is shown in Fig. 1. As Fig. 1 tells us that the efficiency increases with increase in the output power upto a certain output power. But after a particular value of output power, the efficiency decreases. This happens because after this point the power loss increases more rapidly. The power loss increases more rapidly because it changes in proportion with the square of load current. Hence the efficiency decreases after reaching the maximum value.
The output power at full load
\[=\text{}{{V}_{2}}{{I}_{2}}\cos \phi \text{ Watts}\]
This can be expressed in terms of kVA rating as,
Output power at full load
\[=\text{}(kVA\text{ }\times \text{ }\cos {{\phi }_{2}}\text{ }\times \text{ }1000)\text{ Watts}\]
If the full load copper loss is denoted by Pcu(FL) and iron loss by Pi then the efficiency is given by ,
Full load efficiency:
\[{{\text{ }\!\!\eta\!\!\text{ }}_{FL}}=\frac{kVA\times \cos {{\phi }_{2}}\times 1000}{\left( kVA\times \cos {{\phi }_{2}}\times 1000 \right)+ {{P}_{i}}+{{P}_{cu(FL)}}}\]
In this expression, the value of kVA and the copper loss Pcu change with change in load. The iron loss however remain constant The copper loss Pcu will change in square proportion with the load.
The transformer is a static device with no moving parts. Hence the losses due to friction and windage are completely absent. The efficiency of the transformer can be at least equal to 90%.
Effect of frequency on efficiency:
The copper loss is independent of frequency but iron loss increases with increase in frequency. Hence the efficiency decreases with increase in frequency.
Due to the various losses, the power output of the transformer is always less than the corresponding power input to the transformer. Higher the value of this power output (i.e. lesser the losses) for the given input, more efficient is the transformer. Therefore, ordinary or commercial efficiency of the Transformer is defined as the ratio of the output power to the input power (both being in W or kW). It is normally expressed as a percentage. If the copper loss is full-load copper loss, is the full-load secondary current and is the full-load power factor, then the efficiency under full-load condition can be expressed as
\[{{\text{ }\!\!\eta\!\!\text{ }}_{FL}}=\frac{kVA\times \cos {{\phi }_{2}}\times 1000}{\left( kVA\times \cos {{\phi }_{2}}\times 1000 \right)+ {{P}_{i}}+{{P}_{cu(FL)}}}\]
It should be remembered that at 25% load, the value of x will be 0.25, at 50