In this topic, you study Magnetic Hysteresis & Hysteresis Loop.
Magnetic Hysteresis is a very important magnetic property exhibited by ferromagnetic material. This property may be studied by considering a ring shaped unmagnetized test piece of magnetic material.
Connect the terminals of its winding to a battery (E) through a reversing switch (Sw), an ammeter and a variable resistor (R) as shown in Fig. 1.
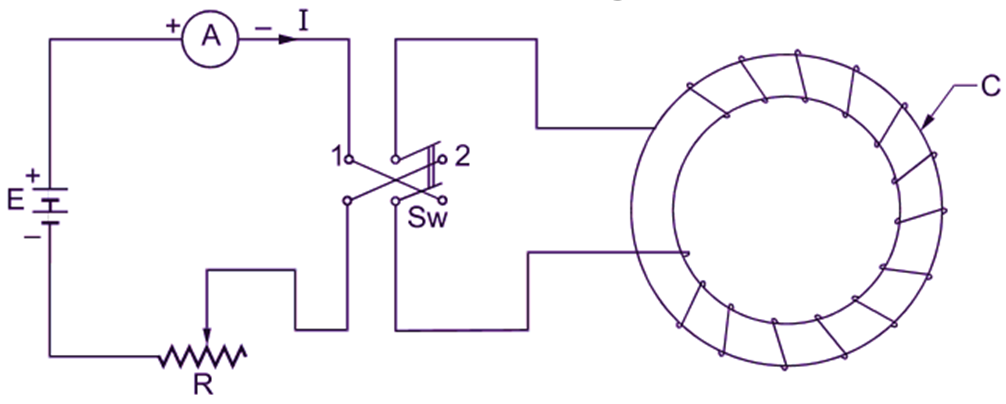
Fig. 1: Determination of the hysteresis loop for the magnetic material
Closing the reversing switch in either Position – 1 or 2, increase the current in the winding from zero to some maximum value. Measure the flux or flux density for different values of the exciting current with the help of some special instruments. If the values of flux density are plotted against the corresponding values of magnetic field strength (given by $\text{H = }\frac{\text{NI}}{l}$) then the graph oa as shown in Fig. 2 is obtained. We know that this graph is nothing but the normal magnetization curve for the magnetic material of the test piece. Now, let the value of H be gradually reduced to zero by reducing the exciting current in the coil to zero. Then, it will be observed that the original curve oa is not retraced but the flux density follows the curve ab. Thus, when H is zero, B has some finite value Br (represented by ob). It means that even if the exciting current in the coil is reduced to zero, the test piece is not completely demagnetized.
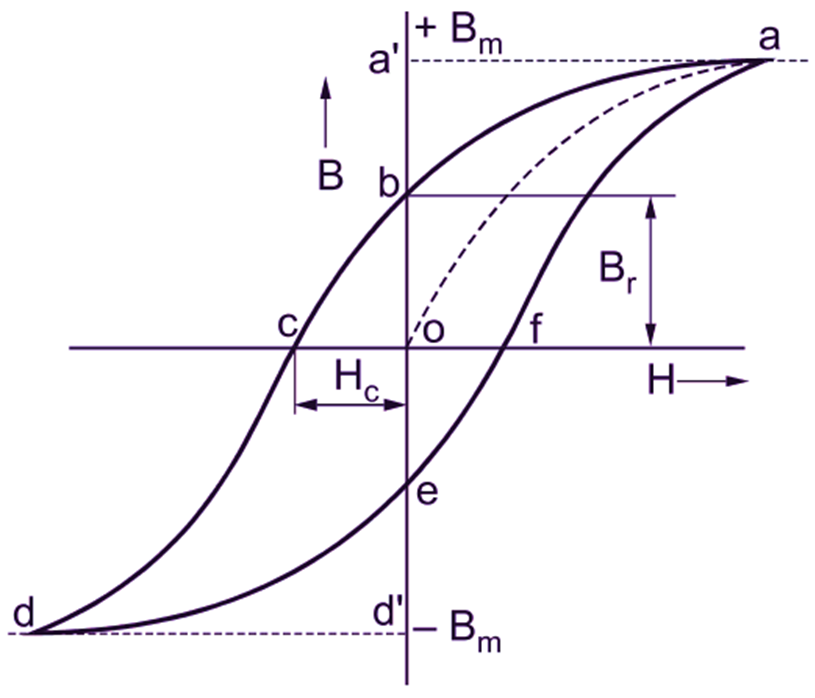
Fig. 2: Hysteresis loop
The value of flux density (i.e. Br) when exciting current and therefore magnetic field strength is reduced to zero is called remanent or residual flux density and is taken as a measure of the residual magnetism. After this, let us demagnetize the test piece. For this, we will have to pass the current through the coil in the reverse direction. The reversal of the current can be achieved with the help of reversing switch by changing its position. This will gradually reduce the flux density and finally at point c, it will be zero, giving complete demagnetization of the test piece. The corresponding value of the reversed magnetic field strength Hc (represented by oc) required to wipe out the residual magnetism (i.e. to bring remanent flux density to zero) in the ring is called the coercive force. If now, the current and hence the magnetic field strength in this reversed direction is increased to its previous maximum value, it will bring the flux density to its previous maximum value, but in the opposite direction (oa’ = od’ = Bm). The total curve traced out will be thus abcd.
A subsequent reduction of the current to zero and increase to its maximum value in the original direction will cause the curve defa to be traced out forming a closed loop. Thus, with the series of changes in current and therefore in H mentioned above, the test piece of magnetic material initially in a complete y demagnetized state undergoes one complete cycle of magnetization.
Looking at the loop abcdefa, it will be seen that the values of B always lag behind those of H. For example, when H is zero at point b, B has still some finite value (Br). The reason is that under the influence of magnetic field strength, the domains (or molecular magnets) when once turned so that their individual magnetizing effect all act in the same direction tend to remain locked in this position. The amount of stability possessed by the alignment of the domains depends upon the quality of the magnetic material and the treatment it receives during manufacture. Consequently, even if H is reduced, the reduction in B is comparatively small.
The phenomenon of lagging of flux density (B) behind the magnetic field strength (H) when a specimen of ferromagnetic material is taken through a cycle of magnetization is called magnetic hysteresis.
The loop abcdefa which represents the variations of B with H for one complete cycle of magnetization is therefore, called a hysteresis loop
The area of the hysteresis loop and the values of remanent flux density (Br = ob) and coercive force (Hc = oc) are dependent on the peak value of the magnetic field strength. They reach their maximum values when the peak value of the magnetic field strength is sufficiently large to produce saturation of the magnetic material. The value of remanent flux density if magnetic saturation is reached at the tips of the hysteresis loop is known as the retentivity or remanence of the material and the corresponding coercive force is called its coercivity. It should be noted that higher the value of the retentivity or remanence, higher is the power of the magnetic material to retain its magnetism. Similarly, higher the value of the coercivity, higher is the power of the magnetic material to resist its demagnetization.
Practical Importance of Hysteresis Loop
The suitability of the magnetic material for use in a particular application is largely dependent on the area and shape of its hysteresis loop. As an illustration, consider the hysteresis loops for different magnetic materials shown in Fig. 3.
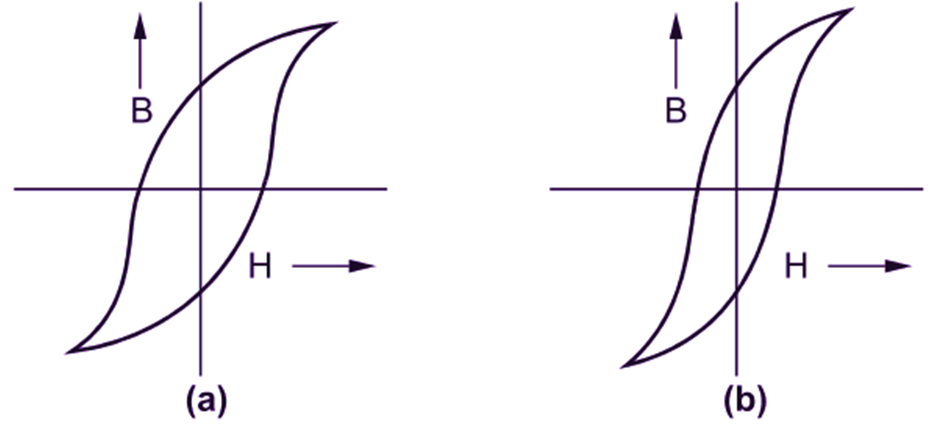
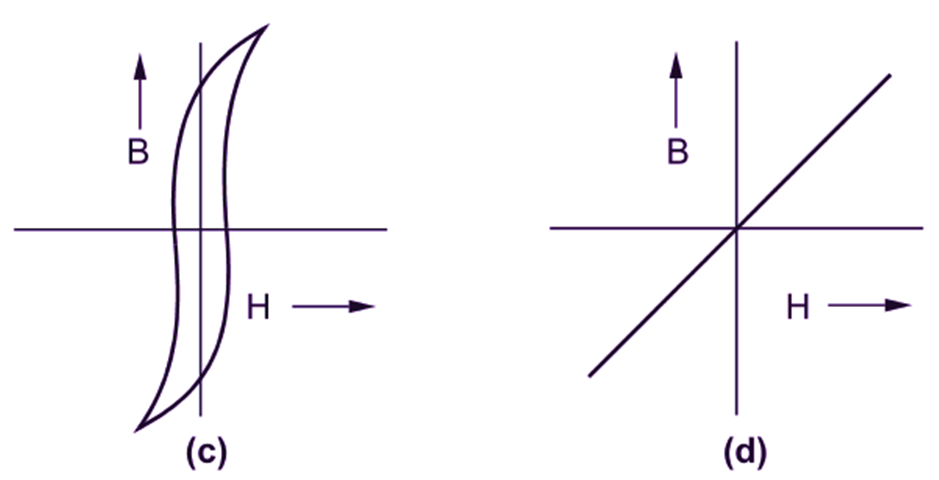
Fig. 3. Shapes of hysteresis loops for different materials (a) Hard steel, (b) Wrought iron, (c) Sheet steel (alloyed with silicon), d Air or non-magnetic material
The material for permanent magnet should have a large hysteresis loop to give both a high remanence and a high coercive force. Hard steel (particularly that containing tungsten, chromium or cobalt) with a large hysteresis loop (Fig. 3 a) is, therefore, suitable for making permanent magnets. Certain alloys of iron, nickel, aluminium andcobalt are stil better. Wrought iron or mild steel has a high permeability and low coercivity as indicated by its hysteresis loop (Fig. 3 b). Hence, it is suitable for electromagnets. The hysteresis loop for sheet steel alloyed with silicon (Fig. 3 c) shows that it has a still higher permeability and lower hysteresis loss. Such materials are most suitable for making those parts Of the electrical equipments which are subjected to rapid reversals of magnetization. Use of these materials under such condition keeps the hysteresis loss low. Thus, the hysteresis loops which reveal the properties of the magnetic materials are of great practical importance. It will be interesting to note that in the case of non-magnetic materials, such as air, the hysteresis loop becomes a single diagonal straight line passing through the origin (Fig. 3 d). The area of the hysteresis loop being zero, there is no hysteresis loss in this case.