When the coils are so connected as to have a common voltage i.e. their startings are connected at one end and their ends are connected at another end across a voltage, these are said to be connected in parallel (Fig. 1).
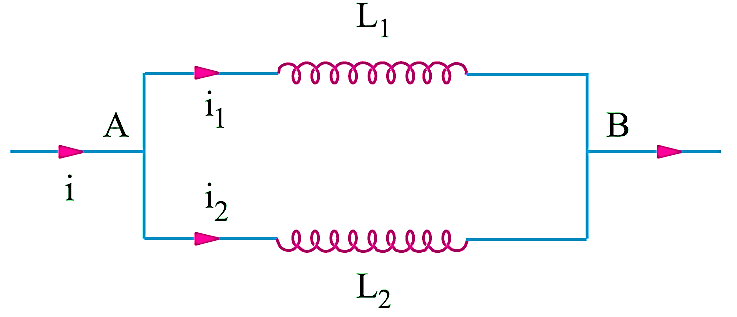
Fig.1: Inductance in Parallel.
Let their inductances be L1 and L2 and are connected across E volt of f frequency. And i be the main supply current also i1 and i2 be the branch currents. Here
\[i={{i}_{1}}+{{i}_{2}}\]
\[\frac{E}{{{X}_{L}}}=\frac{E}{{{X}_{L1}}}+\frac{E}{{{X}_{L2}}}\]
or
\[\frac{E}{2\pi fL}=\frac{E}{2\pi f{{L}_{1}}}+\frac{E}{2\pi f{{L}_{2}}}\]
\[\frac{1}{L}=\frac{1}{{{L}_{1}}}+\frac{1}{{{L}_{2}}}\]
Thus the reciprocal of total inductance is equal to the sum of reciprocal of individual inductances connected in parallel.
In actual practice the flux links or effects the other coil and the coefficient of mutual inductance M, comes into existence,
Then
\[L=\frac{{{L}_{1}}{{L}_{2}}-{{M}^{2}}}{{{L}_{1}}{{L}_{2}}-2M}\]
When the mutual flux helps the individual flux.
\[L=\frac{{{L}_{1}}{{L}_{2}}-{{M}^{2}}}{{{L}_{1}}+{{L}_{2}}+2M}\]
When the mutual flux opposes the individual flux.