In this topic, you study Kirchhoff’s Voltage Law (KVL) – Statement, Explanation & Examples.
This law states that the algebraic sum of all branch voltages around any closed circuit (or mesh) is always zero i.e. Around a closed circuit, ∑V = 0
In other words, according to this law, in any closed circuit, the algebraic sum of all the applied electromotive forces (e.m.f.s) and the products of the current and the resistance of each part of the circuit is always zero i.e.
Around any closed circuit,
\[\sum E.M.F+\sum I.R.=0\]
Explanation of Kirchhoff’s Voltage Law (KVL)
The law is based on the fact that if one starts at a certain point on a closed circuit and goes on noting down the potential changes while travelling in any one particular direction round the circuit until the starting point is reached, then he must be at the same potential with which he started. Therefore, it obviously means that the sum of all the potential rises met on the way must necessarily be equal to the sum of all the potential drops in the various parts of the circuit, thus giving the total change in the potential as zero.
Sign Convention of Kirchhoff’s Voltage Law (KVL)
For app Ying Kirchhoff’s voltage law to a closed circuit, we will have to start from one point on it and note down the potential changes while going round the circuit in any one particular direction (clockwise or anticlockwise) till the starting point is reached again.
During this process, we will have to follow certain sign conventions regarding the potential changes met on the way for making their algebraic addition. The following sign convention can be conveniently adopted:
A rise in potential should be considered as positive. A fall in potential should be considered as negative.
For example, while traversing a source of e.m.f. from its negative terminal to the positive terminal, there is a rise in potential. Hence, in such a condition, this e.m.f. should be considered as positive. On the other hand, while going from the positive terminal of the source to its negative terminal, the potential drops. Naturally, then the e.m.f. will have to be considered as negative. Thus, the direction in which a source of e.m.f. is traversed decides the sign of its e.m.f. and it is independent of direction of current flowing through the branch in which the source is connected.
In the case of a resistor, if we go through it in the direction of the current, then the voltage drops. This is because the current always flows from the point of higher potential to a point of lower potential. Hence, this voltage drop should be taken as negative.
However, while going through the resistor in the direction opposite to that of the current, there is a rise in potential. Therefore, this rise in voltage then should be considered as positive. Thus, it should be noted that the direction of the current flowing through the resistor plays important role in deciding the sign of the change in potential across it.
Illustration of Kirchhoff’s Voltage Law (KVL)
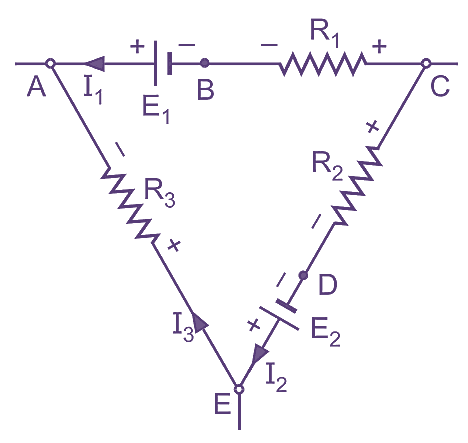
Figure 1.
Consider the closed circuit ABCDEA shown in Fig. 1. Let us apply Kirchhoff’s voltage law to this circuit. For that, with the above mentioned sign convention in mind, if we start from point A and travel round the circuit in say, clockwise direction, following voltages will be met on the way.
- E1 : It is negative since we are proceeding from the positive plate of a cell to its negative plate.
- I1R1 : It is positive since we are traversing the resistance R1 in the direction opposite to that of the current flowing through it.
- I2R2 : It is negative for the reason that we are going through the resistor R2 in the direction of the current flowing through it.
- E2 : It is positive since we are proceeding from the negative plate of a cell to the positive plate.
- I3R3 : It is negative for the reason similar to that mentioned in the earlier case of I2R2.
Then, application of Kirchhoffs voltage law will give the following equation:
\[-{{E}_{1}}+{{I}_{1}}{{R}_{1}}-{{I}_{2}}{{R}_{2}}+{{E}_{2}}-{{I}_{3}}{{R}_{3}}=0\]