In this topic, you study the Memory and Memoryless Systems theory, definition & solved examples.
Let $x(t)$ and $y(t)$ be the input and output signals, respectively, of a system shown in Figure 1. Then the transformation of $x(t)$ into $y(t)$ is represented by the mathematical notation
$y(t) = {\mathbf{T}}x(t)$
where $\mathbf{T}$ is the operator which defined rule by which $x(t)$ is transformed into $y(t)$.
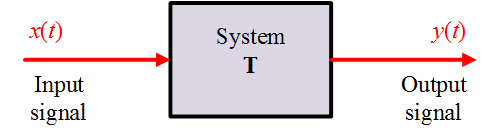
Figure 1: System with a single input and output signal.
Memoryless System
A system is called static if output of system is dependent on present value of input. It is also known as static system. Example of memoryless systems are
\[y(t) = x(t)\]
\[y(t) = tx(t) + 2x(t)\]
Memory System
A system is called dynamic if output of system dependents on past or future values of input at any instant of time. It is also known as dynamic. Example of dynamic systems are
\[y(t) = x(t + 1)\]
\[y(t) = tx(t) + x(t – 1)\]
Example : Determine whether or not each of the following systems are memoryless with input $x(t)$ and output $y(t)$.
(i) \[y(t) = x(3t)\]
(ii) \[y(t) = x(-t)\]
(iii) \[x(\cos t)\]
Solution : (i) \[y(t) = x(3t)\]
put $ t = 1$
\[ y(1) = x(3) \]
hence the system with memory as output $y(1)$ depends on future input $x(3)$.
Solution : (ii) \[y(t) = 5x(t)\]
put $t$ = 1
\[ y(1) = 5x(1) \]
hence the system is memoryless as output $y(1)$ depends on present input $x(1)$.
Solution : (iii) \[x(\cos t)\]
put $t$ = 0
\[ y(0) = x(1) \]
hence the system with memory as output $y(0)$ depends on future input $x(1)$.