In this topic, you study the definition, theory, formula, derivation & diagram of ammeter shunt resistance.
The shunt resistance is essentially a low value resistance connected in parallel to the ammeter. It is used to extend the range of an ammeter.
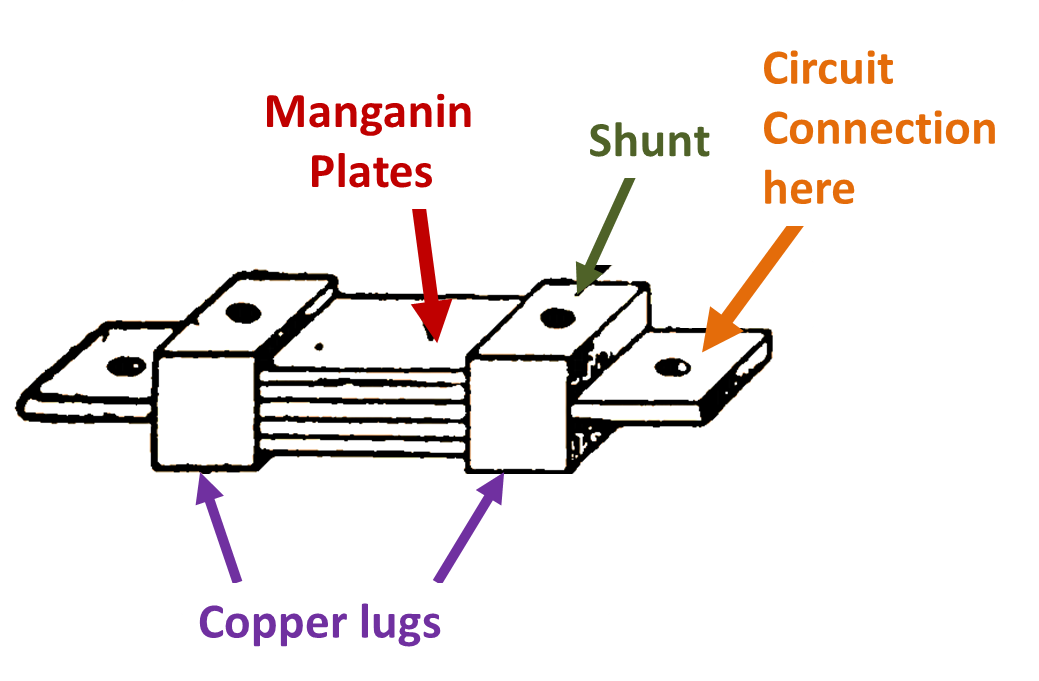
Fig.1: Shunt Resistance.
Let there be an instrument (Galvanometer) as shown in Fig. 2 connected in series with a load and supply.
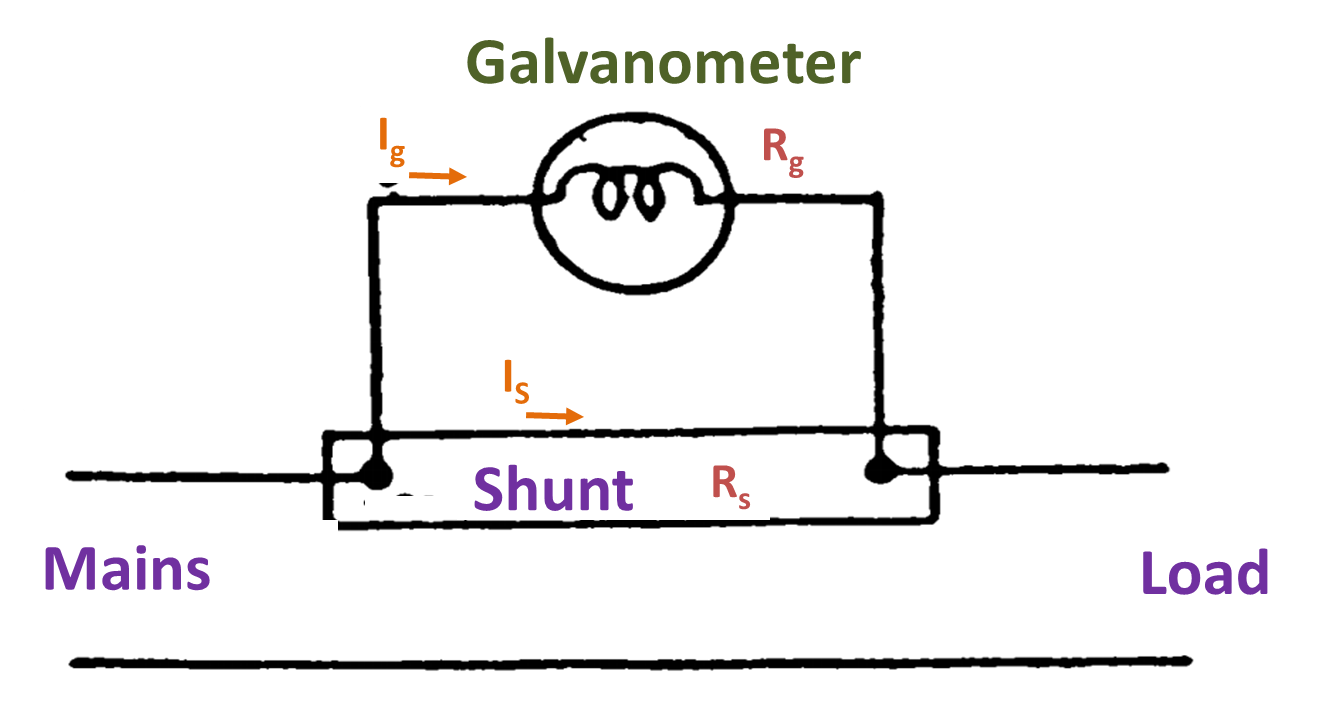
Fig. 2: Shunt Resistance circuit diagram
Rg = Resistance of the galvanometer in Ohm,
RS = Resistance of the shunt in Ohm,
IS = Current in shunt in Amp,
Ig = Current in the galvanometer in Amp.
Let the total current is I Amp, which is
\[\text{I }=\text{ }{{\text{I}}_{\text{g}}}+\text{ }{{\text{I}}_{\text{S}}}\text{ Amp}\]
\[{{\text{I}}_{\text{S}}}\text{ }=\text{ (I}-\text{ }{{\text{I}}_{\text{S}}}\text{) Amp}\]
The voltage drop in the shunt and galvanometer is same so
\[{{\text{I}}_{\text{g}}}\text{ }{{\text{R}}_{\text{g}}}=\text{ }{{\text{I}}_{\text{S}}}\text{ }{{\text{R}}_{\text{S}}}\]
Now substituting for IS
\[{{\text{I}}_{\text{g}}}\text{ }{{\text{R}}_{\text{g}}}=\text{ (I}-\text{ }{{\text{I}}_{\text{g}}}\text{) }{{\text{R}}_{\text{S}}}\]
and
\[{{\text{R}}_{\text{S}}}=\text{ }\frac{{{\text{I}}_{\text{g}}}\text{ }{{\text{R}}_{\text{g}}}}{\text{(I}-\text{ }{{\text{I}}_{\text{g}}}\text{)}}\text{ Ohm}\]
Also,
\[{{\text{R}}_{\text{S}}}=\text{ }\frac{{{\text{I}}_{\text{g}}}\text{ }{{\text{R}}_{\text{g}}}}{\text{(I / }{{\text{I}}_{\text{g}}}-\text{ 1)}}\text{ Ohm}\]
$\text{I / }{{\text{I}}_{\text{g}}}\text{ }$ is known as the multiplying factor.
Similarly
\[{{\text{I}}_{\text{g}}}\text{ }{{\text{R}}_{\text{g}}}=\text{ I }{{\text{R}}_{\text{S}}}-\text{ }{{\text{I}}_{\text{g}}}\text{ }{{\text{R}}_{\text{S}}}\]
or
\[\text{I }{{\text{R}}_{\text{S}}}=\text{ (}{{\text{R}}_{\text{S}}}+\text{ }{{\text{R}}_{\text{g}}}\text{) }{{\text{I}}_{\text{g}}}\]
or
\[\frac{\text{I}}{{{\text{I}}_{\text{g}}}}=\text{ }\frac{{{\text{R}}_{\text{S}}}+\text{ }{{\text{R}}_{\text{g}}}}{{{\text{R}}_{\text{S}}}}=\text{ }\frac{{{\text{R}}_{\text{g}}}}{{{\text{R}}_{\text{S}}}}+\text{ 1}\]
This is also known as the multiplying factor or the instrument constant and is equal to $\frac{{{\text{R}}_{\text{g}}}}{{{\text{R}}_{\text{S}}}}+\text{ 1}$
(Hence the circuit current) = (Full scale deflection of the instrument × Instrument constant)
Example. A M. C. type instrument gives full scale deflection 15 mA and has a resistance of 3 Ω. Calculate the resistance to be connected to use this meter up to 500 m4 ammeter.
Solution. The galvanometer has the resistance of 3 Ω and the full scale deflection is 15 mA. When it is used as an ammeter 0 – 500 mA. The total current is 500 mA so the current to bypass through shunt is
500 – 15 = 485 mA
The voltage drop across both will be same, so
\[{{\text{R}}_{\text{S}}}=\text{ }\frac{{{\text{I}}_{\text{g}}}\text{ }{{\text{R}}_{\text{g}}}}{{{\text{I}}_{\text{S}}}}\]
\[{{\text{R}}_{\text{S}}}=\text{ }\frac{\text{15 }\times \text{ 1}{{\text{0}}^{-3}}\times \text{ 3}}{\text{485 }\times \text{ 1}{{\text{0}}^{-3}}}=\text{ }0.093\text{ }\Omega \]