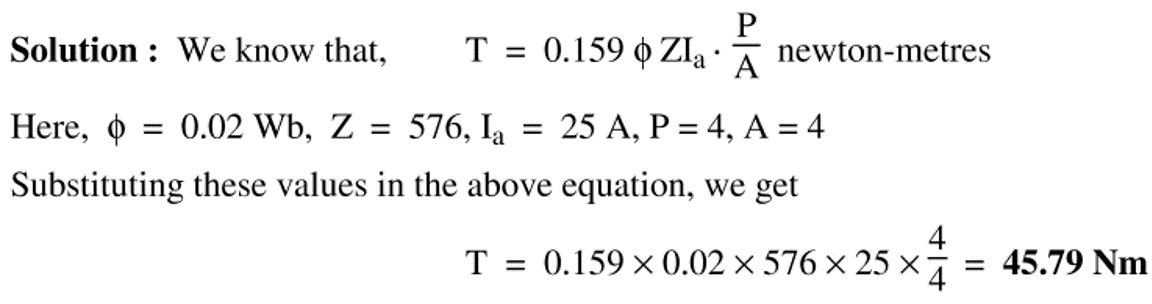In this topic, you study Torque Equation of a DC Motor.
In a dc motor, each armature conductor by virtue of the force experienced by it, exerts a torque tending to turn the armature (Fig. 1).

Fig. 1: Torque on motor armature
The sum of all these torques due to individual conductors is called gross or armature torque (T). Let us now derive the expression for this torque. For this, let
Φ = Flux per pole, in webers
Z = Total number of armature conductors
la = Total armature current, in amperes
P = Number of poles
A = Number of parallel paths in the armature winding
D = Diameter of the armature, in metres
L = Length of the armature, in metres (giving the effective length of each armature conductor)
Then, Average flux density under a pole face,
\[\text{B}=\frac{\text{P}\phi }{\text{ }\!\!\pi\!\!\text{ DL}}\text{ teslas}\]
Current per armature conductor,
\[\text{I}=\frac{{{\text{I}}_{\text{a}}}}{\text{A}}\text{ amperes}\]
Force on each armature conductor,
\[\text{F}=\text{BIl}=\frac{\text{P}\phi }{\text{ }\!\!\pi\!\!\text{ DL}}\cdot \frac{{{\text{I}}_{\text{a}}}}{\text{A}}\cdot \text{L}\]
\[=\frac{\text{P}\phi {{\text{I}}_{\text{a}}}}{\text{ }\!\!\pi\!\!\text{ DA}}\text{ newtons}\]
Hence, Torque due to each conductor
\[\text{= F}\times \frac{\text{D}}{\text{2}}=\frac{\text{P}\phi {{\text{I}}_{\text{a}}}}{\text{ }\!\!\pi\!\!\text{ DA}}\times \frac{\text{D}}{\text{2}}\]
\[=\frac{\text{P}\phi {{\text{I}}_{\text{a}}}}{\text{2 }\!\!\pi\!\!\text{ A}}\text{ newton-meters}\]
∴ Toatl armature torque,
\[\text{T = }\left( \frac{\text{P}\phi {{\text{I}}_{\text{a}}}}{\text{2 }\!\!\pi\!\!\text{ A}} \right)\times \text{Z}\]
\[\text{= }\frac{\text{1}}{\text{2 }\!\!\pi\!\!\text{ }}\text{ }\phi \text{ Z }{{\text{I}}_{\text{a}}}\cdot \frac{\text{P}}{\text{A}}\]
\[\text{= 0}\text{.159 }\phi \text{ Z }{{\text{I}}_{\text{a}}}\cdot \frac{\text{P}}{\text{A}}\text{ newton-meters}\]
For a particular machine, Z, P and A being fixed,
\[\text{T}\propto \phi \cdot {{\text{I}}_{\text{a}}}\]
Thus, it should be noted that the torque of a dc motor is proportional to the product of the flux per pole and the armature current.
Shaft Torque: The whole of the torque developed by the armature is not available at the shaft for doing useful work since a part of it is used in overcoming the friction, windage and iron losses. The torque which is available at the shaft for doing useful work is known as shaft torque (Tsh). The net power output of the motor in horse power obtained by using its shaft torque is called brake horse power (B.H.P.) and given by
\[\text{B}\text{.H}\text{.P}\text{. }\left( \text{metric} \right)=\frac{{{\text{T}}_{\text{sh}}}\times (\text{2 }\!\!\pi\!\!\text{ N/60)}}{\text{735}\text{.5}}\]
where = Speed of the motor, in r.p.m.
Example 1: A 4-pole dc. motor has lap connected armature winding with 576 conductors and draws an armature current of 25 A. If the flux per pole is 0.02 Wb, calculate the gross torque developed by the motor.
Solution: