Two Wattmeter Method of power measurement can be used for both the balanced or unbalanced loads of 3 Φ 4 wires or 3 Φ 3 wire systems. In this method two wattmeters are connected as shown in Fig. 1. The current coils are connected in series with the load and the pressure coils are connected across the line voltage. The total power consumed by the load is the algebraic sum of both wattmeters reading keeping in view the value of power factor of the load i.e.
p = W1 + W2
In this method, the current coil of the two wattmeters are connected in any of the two lines and the potential coil of both wattmeters are connected with the left third line, in which no wattmeter is connected.
Star Connected Load
The Fig. 1. shows arrangement of wattmeter for a 3-phase star connected load.
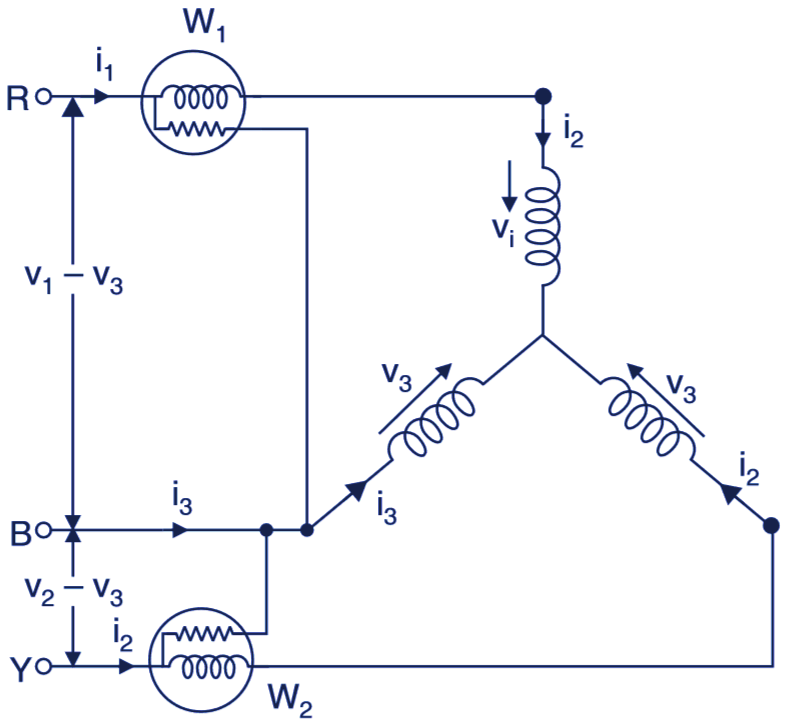
Fig. 1. Two Wattmeter Method for Star Connected Load.
Let v1, v2, v3 are the instantaneous voltages and i1, i2, and i3 are the instantaneous value of currents. As, these are the instantaneous values therefore, instantaneous power will be equal to the sum of their products i.e., instantaneous power
p = v1 i1 + v2 i2 + v3 i3 . . .(i)
It can be proved, that the total power will be the algebraic sum of the readings of the two wattmeters. If readings of the wattmeters are W1 and W2, the total power = W1 + W2.
Proof: Since all the three phases meet at a star point, according to the Kirchoff’s currents law (KCL), the algebraic sum of the currents will be zero. i.e.,
i1 + i2 + i3 = 0
or
i3 = – (i1 + i2) . . .(ii)
Substituting this value in expression (i). The Instantaneous total power will be
p = v1 i1 + v2 i2 + v3 (i1 + i2)
= v1 i1 + v2 i2 – v3 i1 – v3 i2
p = i1 (v1 – v3) + i2 (v2 – v3) . . .(iii)
As i1 is the instantaneous current flowing through the current coil of wattmeter w1 and (v1 – v3) is the potential difference acting across its potential coil hence,
i1 (v1 – v3) = W1
Similarly, i2 is the instantaneous current flowing through the current coil of wattmeter W2 and (v2 – v3) is the potential difference acting across its potential coil hence.
i2 (v2 – v3) = W2
Hence, total instantaneous power,
p = W1 + W2
Delta Connected Load
The Fig. 2 shows wattineters connections for 3-phase delta connected load.
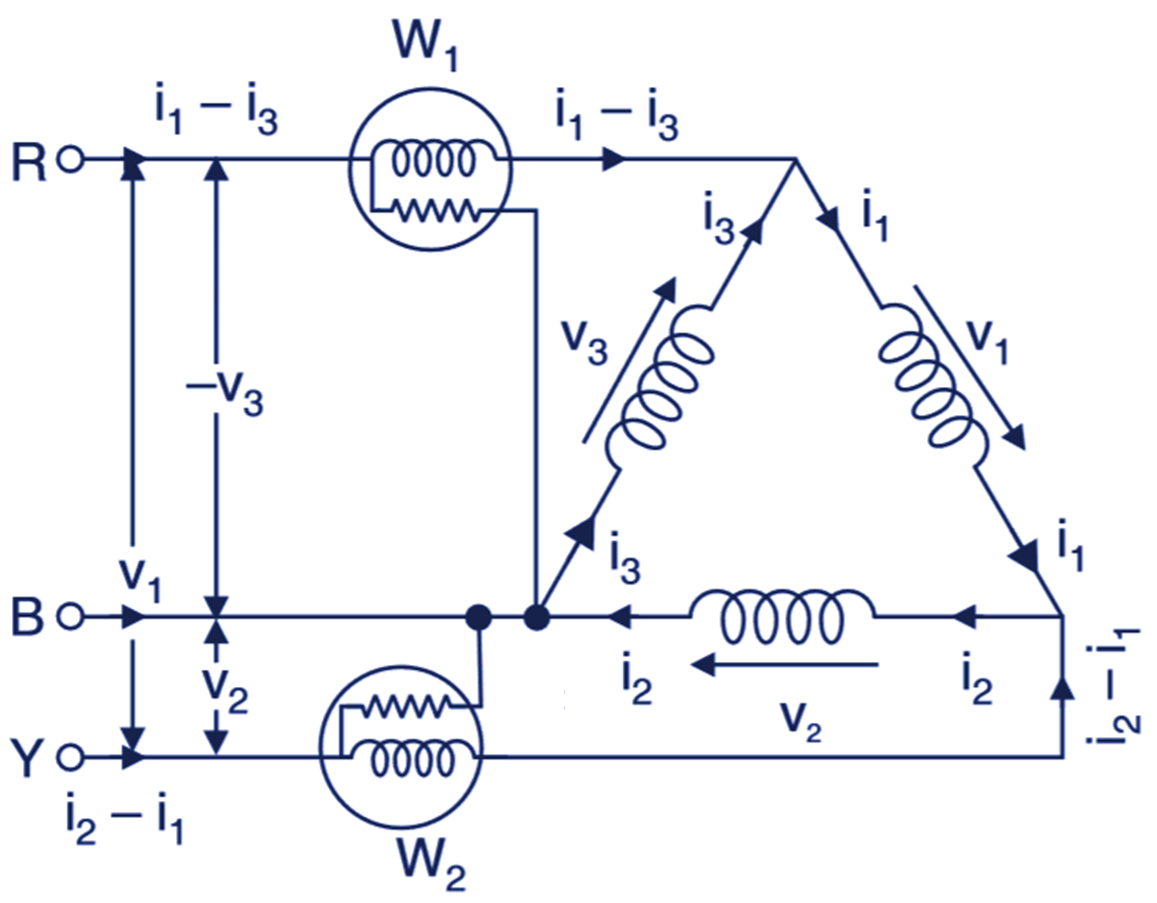
Fig. 2. Two Wattmeter Method for Delta Connected Load
In delta, as the three phases form a closed ioop and according to the Kirclioff voltage law (KVL)
v1 + v2 + v3 = 0
or
v1 = – (v2 + v3)
The Instantaneous total power will be
p = v1 i1 + v2 i2 + v3 i3 . . .(iv)
Substituting in eq. (iv) v1 = – (v2 + v3) we get
p = – (v1 – v3) i1 + v2 i2 + v3 i3
p = – v3 (i1 – i3) + v1 (i2 – i1) . . .(v)
As – v3 is the instantaneous potential difference across potential coil of wattmeter W2 and (i1 – i3) is the instantaneous current flowing through its current coil hence.
– v3 (i2 – i3) = W1
Similarly, v1 is the instantaneous potential difference across the potential coil of wattmeter W2 and (i2 – i1) is the instantaneous current flowing through its current coil hence,
v1 (i2 – i1) = W2
Hence, total instantaneous power [(From eq. (v)]
p = W1 + W2
Result: Hence, the algebraic sum of two wattmeters’ readùigs give the total power of the circuit irrespective that it is star or delta connected or it is balanced or unbalanced.
Depending upon the power factor, the readings of the wattmeters are affected. There are the following different cases.
(i) When power factor is unity. In this case both the wattmeters will give positive readings and equal also.
(ii) When Power factor ≥ 0.5. Both wattmeters will read positive but different readings. In case if the power factor is 0.5, only one wattmeter will give reading and total power will be equal the this reading.
(iii) When power factor < 0.5. In this case the one wattmeter will read in opposite direction, change the connection of the current coil of this wattmeter and get positive reading.