After reading this topic Type 0 system with step, ramp and parabolic input in the control system, you will understand the theory, steady state error expression, and derivation.
Consider a simple closed loop control system with negative feedback as shown below in Figure 1.
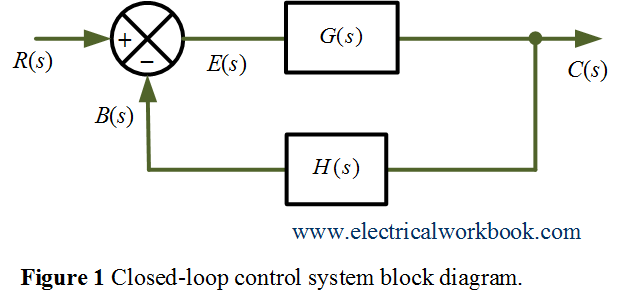
where R(s) is the input signal, B(s) is the feedback signal, C(s) is the output signal, G(s) is the forward gain, H(s) is the feedback gain and error signal E(s) is the difference between input R(s) and feedback signal B(s).
As we know steady-state error depends on,
- input signal R(s)
- open-loop transfer function G(s)H(s) or type the system.
The general form of the open-loop transfer function G(s)H(s) is
\[G(s)H(s) = \frac{{K(1 + s{T_a})(1 + s{T_b})…}}{{{s^j}(1 + s{T_1})(1 + s{T_2})…}}….(1)\]
So, type of the system depens on j i.e, For type 0 system j = 0, type 1 system j = 1 and so on.
Type 0 system with Step Input
For a type 0 system j = 0, using Equation 1 the open-loop transfer function G(s)H(s) is given by
\[G(s)H(s) = \frac{{K(1 + s{T_a})(1 + s{T_b})…}}{{(1 + s{T_1})(1 + s{T_2})…}}….(2)\]
For step Input, the static position error constant ${K_p}$ is given by
\[{K_p} = \mathop {\lim }\limits_{s \to 0} G(s)H(s)….(3)\]
Using Equation 2 and Equation 3 gives,
\[{K_p} = \mathop {\lim }\limits_{s \to 0} \frac{{K(1 + s{T_a})(1 + s{T_b})…}}{{(1 + s{T_1})(1 + s{T_2})…}} = K\]
The steady-state error is given as
\[{e_{ss}} = \frac{A}{{1 + {K_p}}}\]
Therefore, as shown in Figure 1 for a type 0 system with step input, the steady-state error will be
\[{e_{ss}} = \frac{A}{{1 + K}}\]
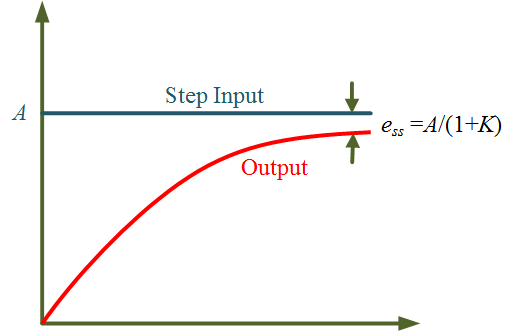
Figure 2 Steady-state error in Type 0 system with Step Input.
Type 0 system with ramp Input
For ramp Input, the static velocity error constant ${K_v}$ is given by
\[{K_v} = \mathop {\lim }\limits_{s \to 0} sG(s)H(s)….(4)\]
Using Equation 2 and Equation 4 gives,
\[{K_v} = \mathop {\lim }\limits_{s \to 0} s\frac{{K(1 + s{T_a})(1 + s{T_b})…}}{{(1 + s{T_1})(1 + s{T_2})…}}\]
\[ = 0\]
The steady-state error is given as
\[{e_{ss}} = \frac{A}{{{K_v}}}\]
Therefore, as shown in Figure 3 for a type 0 system with ramp input, the steady-state error will be
\[{e_{ss}} = \frac{A}{0} = \infty \]
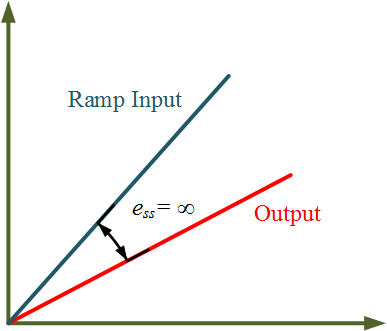
Figure 3 Steady-state error in Type 0 system with Ramp Input.
Type 0 system with parabolic Input
For parabolic Input, the static acceleration error constant ${K_a}$ is given by
\[{K_a} = \mathop {\lim }\limits_{s \to 0} {s^2}G(s)H(s)….(5)\]
Using Equation 2 and Equation 5 gives,
\[{K_a} = \mathop {\lim }\limits_{s \to 0} {s^2}\frac{{K(1 + s{T_a})(1 + s{T_b})…}}{{(1 + s{T_1})(1 + s{T_2})…}}\]
\[ = 0\]
The steady-state error is given as
\[{e_{ss}} = \frac{A}{{{K_a}}}\]
Therefore, as shown in Figure 4 for a type 0 system with parabolic input, the steady-state error will be
\[{e_{ss}} = \frac{A}{0} = \infty \]

Figure 4 Steady-state error in Type 0 system with Parabolic Input.