What is Wheatstone Bridge? – Definition, Diagram & Theory

In this topic, you study the Wheatstone Bridge method of measuring resistance with neat sketch.

It is the most accurate method of determining the value of unknown resistance because it is a null or balance method. It is used to detect the null or balanced condition. In this bridge four resistances are connected as shown in Fig. 1. The P and Q arms are the ratio arms and ‘S’ the standard variable resistor and ‘R’ as the unknown resistance.

A glavanometer G is connected between B and D terminals of the bridge, and the cell E connected in the circuit. The arrangement is known as the Wheatstone bridge.

The series circuit ABC and ADC are adjusted in such a way by adjusting the available resistance ‘S’ as there is no current in the connected galvanometer. When there is no current through the galvanometer the condition is said the null or balanced condition.

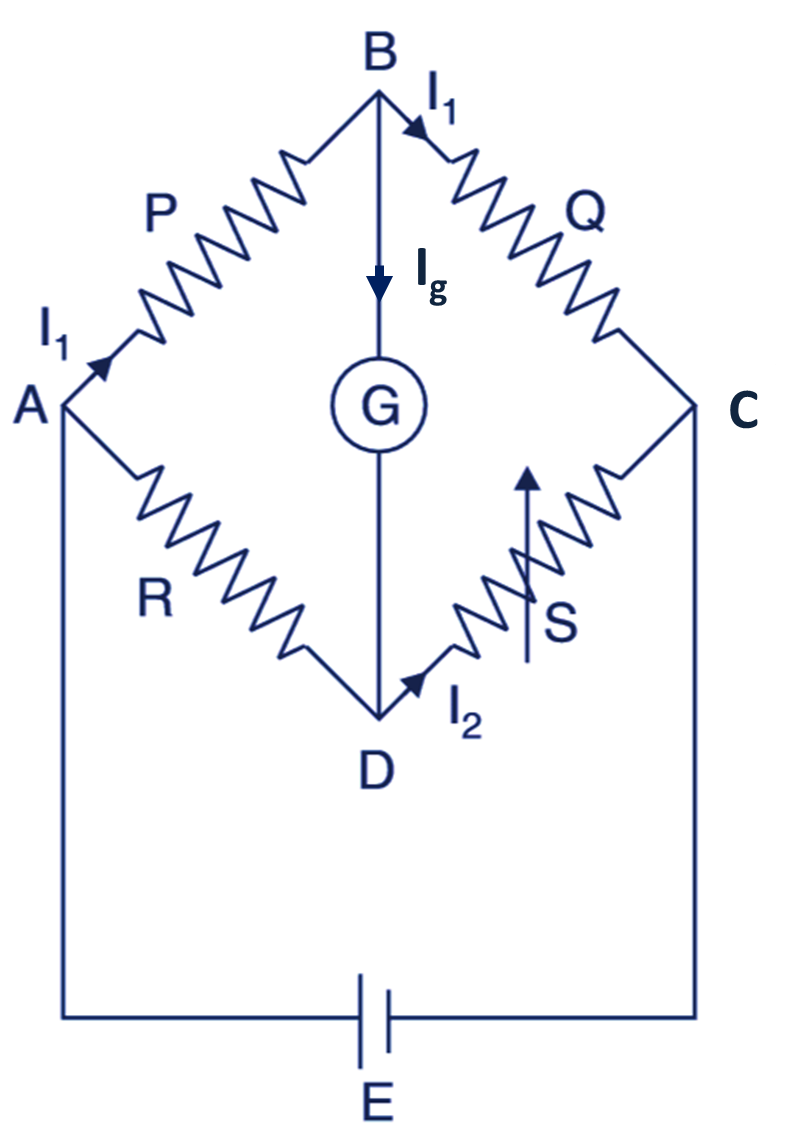
Fig. 1. Wheatstone Bridge

Balanced condition

In case of balanced condition there is no current through the galvanometer i.e., I_g = 0, so the current say I₁ is flowing through P and Q and similarly if I₂ is the current in the ADC circuit than I₂ is flowing through R and S resistances. Thus if there is no current in the galvanometer the point B and D are at the same potential so voltage drop across AB is equal to the voltage drop across AD.

Similarly, voltage drop across BC is equal to the voltage drop across DC i.e.

\[{{\text{I}}_{\text{1}}}\text{P = }{{\text{I}}_{\text{2}}}\text{R}\]

and,

\[{{\text{I}}_{\text{1}}}\text{Q = }{{\text{I}}_{\text{2}}}\text{S}\]

Dividing both

\[\frac{\text{ }{{\text{I}}_{\text{1}}}\text{P}}{{{\text{I}}_{\text{1}}}\text{Q}}\text{ = }\frac{{{\text{I}}_{\text{2}}}\text{R}}{{{\text{I}}_{\text{2}}}\text{S}}\]

or

\[\frac{\text{ P}}{\text{Q}}\text{ = }\frac{\text{R}}{\text{S}}\]

and

\[\text{R = }\frac{\text{ P}}{\text{Q}}\times \text{S}\]

∴ The unknown resistance = Value Of Ratio arms x Known value of variable resistance

The value of ratio arm can be varied by increasing the value of bridge, as well as to obtain greater accuracy. It may be 10, 100, 1000 and 0.1, 0.01, 0.001.

Limitations of Wheatstone Bridge

The wheatstone bridge is not used for measurement of very low resistances, therefore use of wheatstone bridge is limited to the measurement of medium resistances from few ohms upto several megaohms. The upper limit of measurement can be extended further by increasing battery emf E but it can cause over heating of the arms. But the lower limit of measurement is restricted by the resistance of the connecting leads. The error caused by the resistance of the leads may however also be corrected to some extent but in no way, the bridge is suitable to measurement of resistances less than 1 ohm.

Errors in Wheatstone Bridge

Though, Wheatstone bridge is convenient and simple method, its main errors are:

1. Human errors such as finding balance point, taking readings and making calculations.
2. There is a change of value of resistance due to self heating.
3. If the sensitivity of the galvanometer is not sufficient, the balance point will not be exact.
4. The errors due to resistances of leads and contacts.

Problems and Solution on Wheatstone Bridge

Problem 1. The arms of a Wheatstone bridge are P = 100 Ω, Q = 10 Ω, and S = 50 Ω. Determine the unknown resistance R.

Solution:

\[\text{R = }\frac{\text{ P}}{\text{Q}}\times \text{S = }\frac{\text{ }100}{10}\times 500\]

\[\text{R = }500\text{ }\Omega \]