In this topic, you study Series Circuit – Definition, Diagram, Formula & Theory.
A series circuit consists of several resistances, connected one after the other in such a way that they form a chain (Fig. 1).
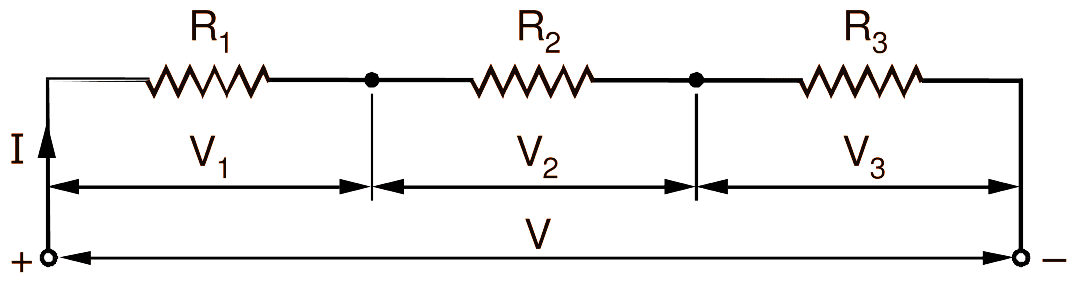
Fig. 1: Series combination Of resistances.
Naturally, current flowing through each resistance is same when the combination is connected across the supply source. For example: The small electrical lights which are placed on a Christmas tree are really a number of resistors joined in series.
Current and Voltage Distribution in Series Circuit
Consider the three resistances R1, R2 and R3 connected in series as shown in Fig. 1. Let the current drawn by this series combination be I amperes when a potential difference of V volts is applied across its terminals. Let V1, V2, and V3 be the voltage drops across R1, R2 and R3 respectively.
\[V={{V}_{1}}+{{V}_{2}}+{{V}_{3}}\]
\[=I{{R}_{1}}+I{{R}_{2}}+I{{R}_{3}}\]
But
\[V=IR\]
Where R is the equivalent of the three resistances in series.
Hence,
\[IR=I{{R}_{1}}+I{{R}_{2}}+I{{R}_{3}}\]
Dividing each term by I, we get,
\[R={{R}_{1}}+{{R}_{2}}+{{R}_{3}}\]
In general, if the number of resistances connected in series is n, then,
\[R={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+….{{R}_{n}}\]
In general, if the number of resistances connected in series is n, then,
\[R={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+….{{R}_{n}}\]
The various results obtained can be summarized as below:
(i) The same current (I) flows through each resistance in turn. (ii) The supply voltage (V) is equal to the sum of the individual voltage drops across the resistances. (iii) The equivalent resistance of a number of resistances joined in series is equal to the sum of the values of the individual resistances.
Further, it follows that if n resistors Of the same resistance value, say r, are connected in series, then their total resistance will be given by
\[R=n.r\]