Capacitors in Parallel – Derivation, Formula & Theory

In this topic, you study Capacitors in Parallel – Derivation, Formula & Theory.

Now, consider three capacitors, having capacitances C₁, C_2, and C₃ farads respectively, connected in parallel across a d.c. supply of V volts, through a switch S_w, as shown in Fig. 1. When the switch S_w is closed, all the capacitors in parallel are charged to have a p.d. of V volts between their plates.

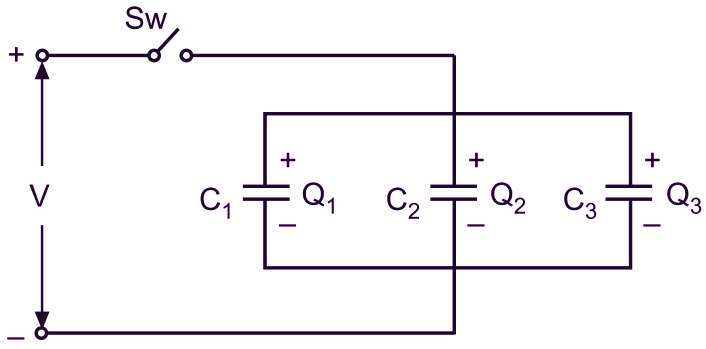
Fig. 1: Capacitors in parallel.

Let Q₁, Q_2, and Q₃ be the charges acquired by the capacitors with capacitances C₁, C_2, and C₃ respectively. Then, obviously,

Q₁ = C₁ V

Q₂ = C₂ V

and,

Q₃ = C₃ V

If Q coulombs is the total resulting charge,

Q = Q₁ + Q₂ + Q₃

Q = C₁ V + C₂ V + C₃ V  ….(1)

But, if C is the capacitance of an equivalent single capacitor for the three given capacitors in parallel, acquiring the same total charge of Q coulombs when the same p.d. of V volts is applied across its terminals, then

Q = C V  ….(2)

Hence, from Equation (1) and Equation (2),

C V = C₁ V + C₂ V + C₃ V

∴

C = C₁ + C₂ + C₃

In general, if the number of capacitors in parallel is n, then

C = C₁ + C₂ + C₃ + …. + C_n

The various results obtained in respect Of a parallel combination Of capacitors can be summarized as below:

(i) After charging, the same potential difference (equal to the supply voltage) is established across all the capacitors.

(ii) The total resulting charge on the combination is equal to the sum of the charges acquired by the individual capacitors i.e.

Q = Q₁ + Q₂ + Q₃ + ….

(iii) The equivalent capacitance Of a number Of capacitors in parallel is equal to the sum of their individual capacitances i.e.

C = C₁ + C₂ + C₃ + …. + C_n

Example 1: Three capacitors have capacitances of 2 μF, 5 μF, and 10 μF respectively. Find the resultant capacitance when they are connected in parallel.

Solution:

In Parallel Connection:

C = C₁ + C₂ + C₃

C = 2 + 5 + 10 = 17 μF