When the coils are so connected that the end of coil one is connected to the starting of second coil and so on as to form a shape of a chain, these are connected in series. In this case the flux of first coil does not effect the second coil at all.
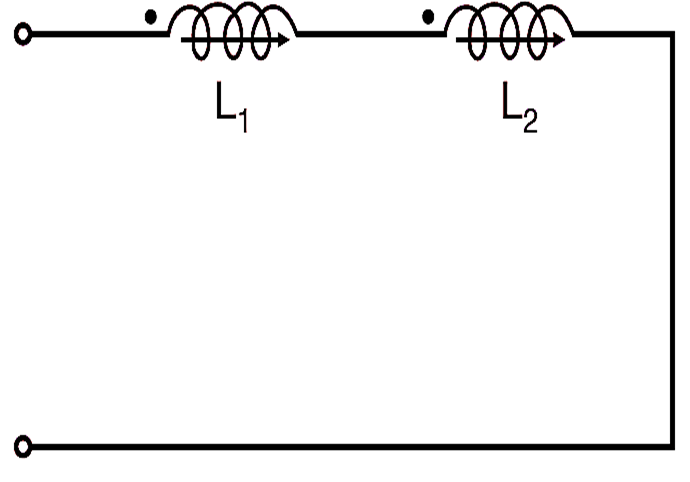
Let their inductances be L1 and L2 are connected across E volt of f frequency. In that case when same current is flowing in both coils (Fig. 1). And E1 and E2 are voltage across inductors L1 and L2 respectively. Then,
\[E={{E}_{1}}+{{E}_{2}}\]
also
\[E=I\times {{X}_{L}}\]
or
\[{{E}_{1}}=I\times {{X}_{L1}}\]
\[{{E}_{2}}=I\times {{X}_{L2}}\]
Than
\[I\times {{X}_{L}}=I\times {{X}_{L1}}+I\times {{X}_{L2}}\]
\[{{X}_{L}}={{X}_{L1}}+{{X}_{L2}}\]
since,
\[{{X}_{L}}=2\pi fL\]
Thus
\[2\pi fL=2\pi f{{L}_{1}}+2\pi f{{L}_{2}}\]
\[L={{L}_{1}}+{{L}_{2}}\]
It is a very ideal case. But in actual practice the mutual induction takes place and let M be the Coefficient of mutual induction. Than equivalent inductance,
Series-adding
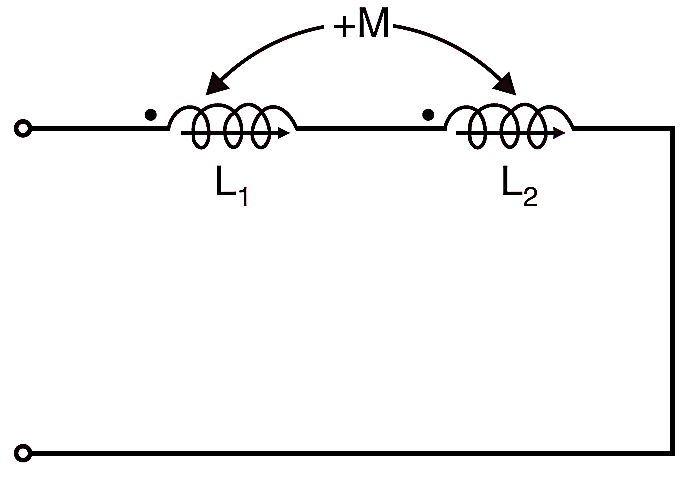
Fig. 1: Inductance in Series (Series-aiding)
If both the coils are connection in such a way as to result in a additive mmfs than equivalent inductance (Fig. 1) is
\[L={{L}_{1}}+{{L}_{1}}+2M\]
Series-opposing
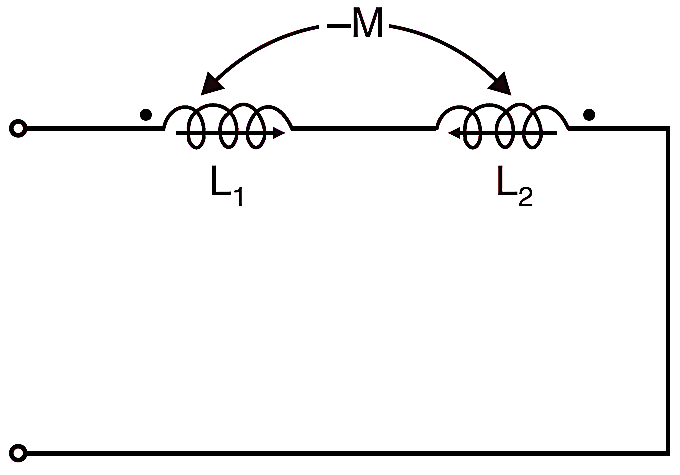
Fig. 2: Inductance in Series (Series-opposing)
If both the coils are connected in such a way as to result in a subtractive mmfs than equivalent inductance (Fig. 2) is
\[L={{L}_{1}}+{{L}_{1}}-2M\]