Carnot engine cycle is a theoretical engine cycle it doesn’t have any practical applications. But it helps in determining the theoretical efficiency of practical engines while designing.
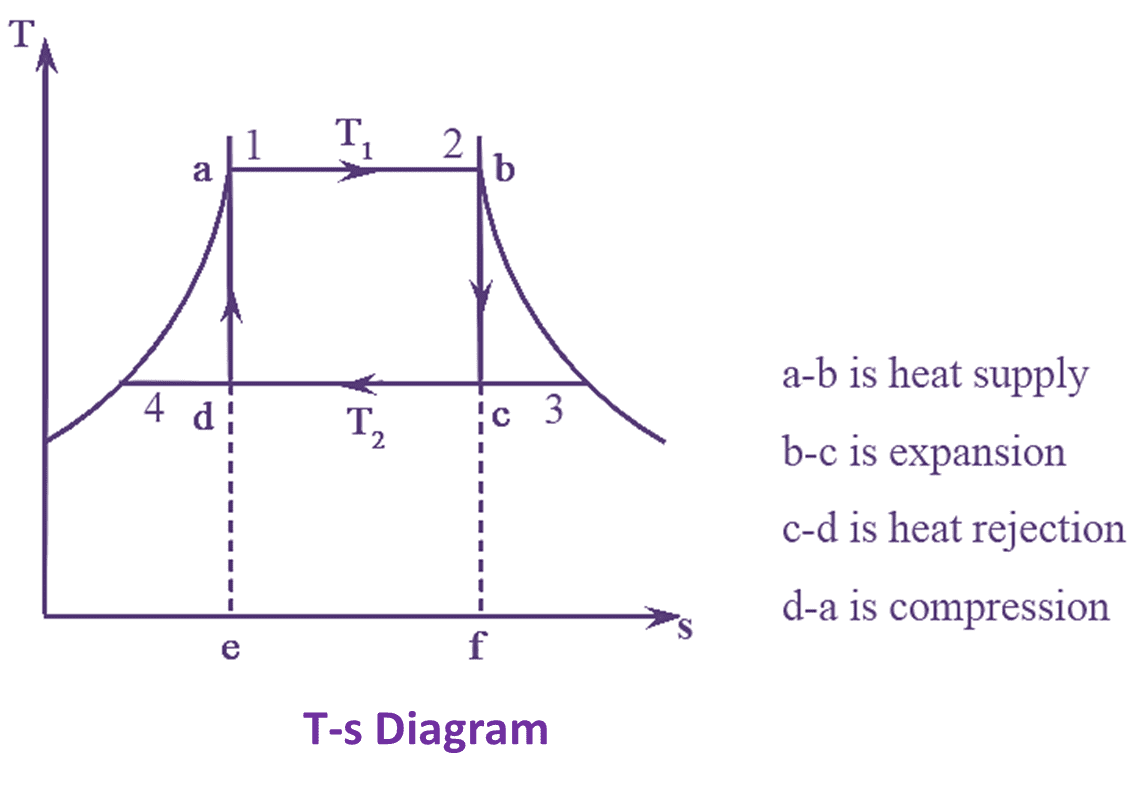
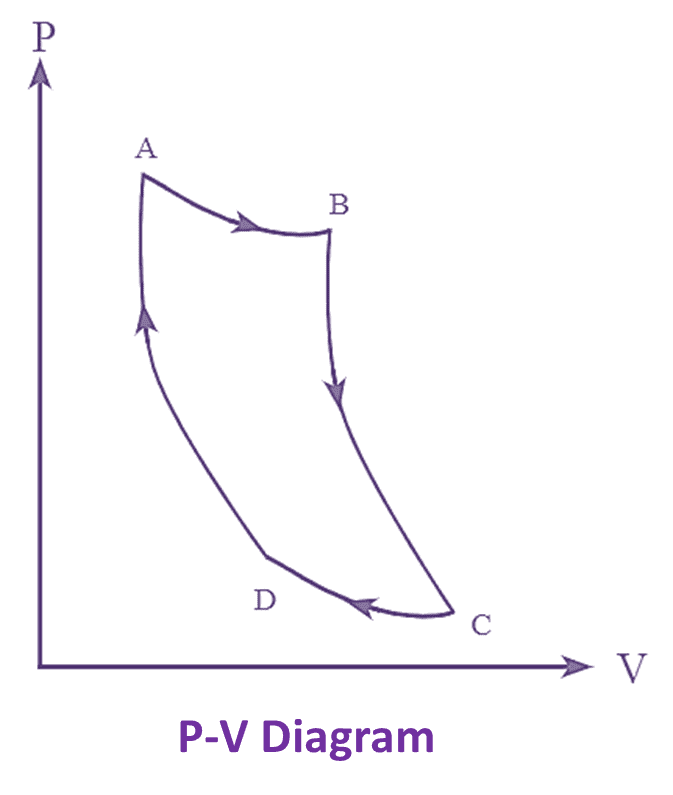
Figure 1 : Carnot Engine T-s Diagram & P-V Diagram.
The Carnot heat engine cycle with T-s and P-V diagrams are shown in the figure 1. The Carnot engine cycle consists of four types of thermodynamic processes in which two are frictionless adiabatic (Isentropic) and the other two are constant temperature operations (Isothermal) processes. These processes operate between the two temperature limits T1 and T2.
In the operation ‘ab’, boiling water is heated at temperature ‘T1’ to obtained a dryness fraction ‘x1’ from the steam. During this operation heat is being absorbed at constant temperature (T1). In the operation ‘bc’, the temperature of the steam decreases isentropically and changes to temperature (T2). The point ‘c’ is the point of steam expansion. Now, the operation shifts to ‘cd’. In this case, the heat is removed at and temperature (T2).
When the steam is completely used it gets cooled down. In the operation ‘dc’. The steam again retains its temperature and pressure through compression and the cycle completes. Now, heat supplied during tile operation ‘ab’ at constant temperature ‘T1’ is given by,
\[\text{Area of abfe}={{T}_{1}}({{S}_{2}}-{{S}_{3}})\]
Heat removed during the operation ‘cd’ at constant temperature is given by,
\[\text{Area of cdef }={{T}_{2}}({{S}_{2}}-{{S}_{3}})\]
During isentropic operation ‘bc’ and ‘da’. There is no heat produced.
Therefore,
Net Workdone = Heat supplied – Heat removed
\[={{T}_{1}}({{S}_{1}}-{{S}_{4}})-{{T}_{2}}({{S}_{2}}-{{S}_{3}})\]
\[=({{T}_{1}}-{{T}_{2}})({{S}_{2}}-{{S}_{3}})\]
The Carnot efficiency is a function of the temperature ‘T1’ and T2 and is given by..
Cannot cycle,
\[\text{ }\!\!\eta\!\!\text{ }=\frac{\text{Workdone}}{\text{Heat supplied}}\]
\[=\frac{({{T}_{1}}-{{T}_{2}})({{S}_{2}}-{{S}_{3}})}{{{T}_{1}}({{S}_{2}}-{{S}_{3}})}\]
\[\text{ }\!\!\eta\!\!\text{ }=\frac{{{T}_{1}}-{{T}_{2}}}{{{T}_{1}}}\]
or
\[\text{ }\!\!\eta\!\!\text{ }=\text{1}-\frac{{{T}_{2}}}{{{T}_{1}}}\]