Cells in Series Combination – Theory, Diagram & Derivation

In this topic, you study theory, diagram & derivation of the cells in a series combination.

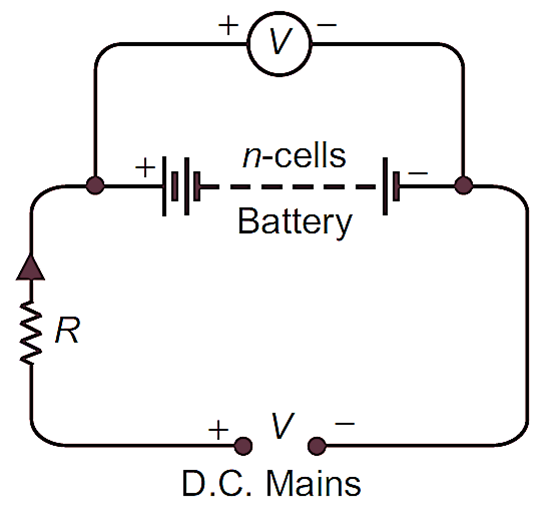
Fig. 1: Cells in series combination.

The combination of cells in which the cells forms a chain shape is known as the series combination. In this system the negative of one cell is connected with the positive of the second cell and so on as shown in Fig. 1. This type of the connections are used when the voltage required is more than the voltage of a cell. So to obtain more voltage the cells are grouped in series. The combination has got the following characteristics:

(i) The voltage of the circuit increases as the number of cells connected in series are increased.

Let,

e = the voltage per cell

r = the internal resistance per cell

E = voltage of the combination

R = the external resistance.

Let there are n cells connected in series, so the e.m.f. will be

= e₁ + e₂ + e₃ + ….. e_n

There are n cells of e volt e.m.f. per cell so,

E = neV  ( e₁ = e₂ = e₃ = …..= e_n)

(ii) The voltage of the combination is equal to the e.m.f per cell multiplied by the number of cell connected in series.

(iii) The total internal resistance increases as more number of cells are added.

The total internal resistance

= r₁ + r₂ + r₃ + ….. r_n

= No. of cells connected x Internal resistance per cell

= n × r ohm.

(iv) The total current Of the combination is same as there is only one path Of the current and

\[=\frac{\text{Total voltage}}{\text{Total resistance}}\]

\[=\frac{\text{No}\text{. of cells  }\!\!\times\!\!\text{  e}\text{. m}\text{.f}\text{. per cell}}{\text{External resistance + Total internal resistance}}\]

\[\text{I}=\frac{\text{ne}}{\text{R + nr}}\text{ amp}\]

Example. Twenty cells each of 1.5 V e.m.f. and internal resistance per cell 0.3 ohm are connected in series. Calculate the current through the external resistance of 20 ohm and also find out the potential difference across it.

Fig. 1.

Solution. The total voltage obtained

= ne = 20 × 1.5 = 30 V

The total internal resistance

= nr = 20 × 0.3 = 6 Ω

Now total resistance R + nr = 20 + 6 = 26 Ω

The current,

\[\text{I}=\frac{\text{ne}}{\text{R + nr}}\text{ amp}\]

\[=\frac{\text{30}}{\text{26}}\text{ = 1}\text{.154 A}\text{.}\]

The potential difference

 = I × R = 1.154  × 20

 = 23.08 V.