An ideal air refrigeration system is assumed to work on reversed Carnot cycle.

Analysis of Reversed Carnot Cycle,
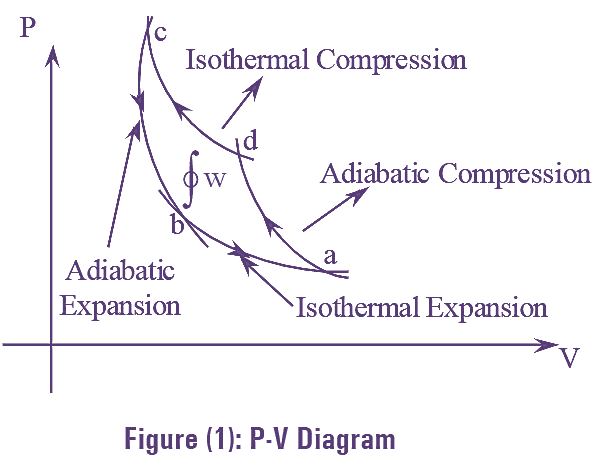
Consider 1 kg of air, taken in a cylinder which is fitted with a piston. Its state is represented by point c.
c-b: Adiabatic Expansion
Air expands adiabatically. Temperature reduces from Tc to Ta.
b-a: Isothermal Expansion
Further expansion of air takes place at constant temperature (Tc). It abstracts heat from the bodies to be cooled.
a-d: Adiabatic Conipression
Air is compressed adiabatically using compressor i.e., work is supplied to air. Temperature rises to Tc.
d-c: Isothermal Compression
Further compression of air takes place at constant temperature (Tc). Air losses heat to any cooling medium.
Ideal COP of the System,
The ratio of refrigeration effect produced by a refrigerating machine in a given tulle to the work supplied during the same time is known as Coefficient of Performance (COP) of the machine.
Let,
R = Refrigerating effect
W = Work input to the machine
\[\text{C}\text{.O}\text{.P}=\frac{R}{W}\]
The coefficient of performance of a refrigeration system is always greater than one. Refrigerating effect per cycle,
$\oint{N}$ = Heat abstracted by air during process ba (From T- s diagram).
= Area under (ba)
\[\oint{N}={{T}_{a}}\times \Delta s\]
Work supplied per cycle,
$\oint{W}$ = Heat rejected by air – Heat abstracted by air
= Area under cb – Area under ba
\[{{T}_{c}}\Delta s-{{T}_{a}}\Delta s=\text{Area cbad}\]
\[\oint{W=}\text{ }({{T}_{c}}-{{T}_{a}})\Delta s\]
Coefficient of performance,
\[\text{C}\text{.O}\text{.P}=\frac{\oint{N}}{\oint{W}}\]
\[=\frac{\text{Heat supplied}}{\text{Workdone}}=\frac{{{T}_{a}}\times \Delta s}{({{T}_{c}}-{{T}_{a}})\times \Delta s}\]
\[\text{C}\text{.O}\text{.P}=\frac{{{T}_{a}}}{{{T}_{c}}-{{T}_{a}}}\]