After reading this topic Field controlled DC Servomotor in the control system, you will understand the theory, derivation, expressions, transfer function, and Block diagram.
Let us consider the Field controlled DC servomotor as shown in Figure 1.
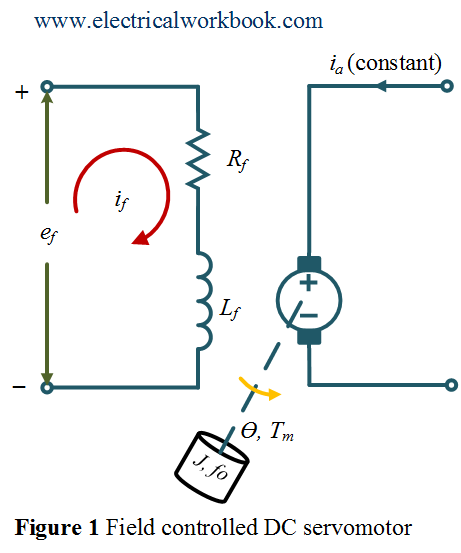
The parameters are taken as
${R_f}$ = Field winding resistance.
${L_f}$ = Field winding inductance.
${i_a}$ = Armature current.
${i_f}$ = Field current.
${e_f}$ = applied field (control) voltage.
${e_b}$ = Motor back emf.
${T_m}$ = torque developed by motor.
$\theta $ = Angular displacement of motor shaft.
$J$ = Equivalent moment of inertia (of load and motor) referred to motor shaft.
$f_o$ = Equivalent viscous friction coefficient of motor and load referred to motor shaft.
In field controlled DC motors, the input field volatge ${e_a}$ controls the motor shaft output while the armature current ${i_a}$ remains constant. The DC motor operates in linear region for servo motor application. Hence, the air-gap flux $\phi $ is proportional of the field current $i_f$ as
\[\phi \propto {i_f}\]
\[\phi = {K_f}\hspace{0.1cm}{i_f}\]
The torque $T_m$ developed by the motor is proportional to the armature current i.e.
\[{T_m} \propto {i_a}\]
Also,
\[{T_m} \propto {K_f}\hspace{0.1cm}{i_f}\hspace{0.1cm}{i_a}\]
\[{T_m} = ({K_1}\hspace{0.1cm}{K_f}\hspace{0.1cm}{i_a})\hspace{0.1cm}{i_f}\]
In field controlled DC motors, the armature current $i_a$ remains constant. Therefore,
\[{T_m} = {{K’}_T}\hspace{0.1cm}{i_f}\]
where, ${{K’}_T}$ is the motor torque constant.
Using KVL on field circuit shown in Figure 1, the differential equation of the field circuit
\[{L_f}\left( {\frac{{d{i_f}}}{{dt}}} \right) + {R_f}\hspace{0.1cm}{i_f} = {e_f}…(1)\]
The torque equation is
\[J\left( {\frac{{{d^2}\theta }}{{d{t^2}}}} \right) + {f_o}\left( {\frac{{d\theta }}{{dt}}} \right) = {T_m} = {{K’}_T}\hspace{0.1cm}{i_f}….(2)\]
Transfer function calculation of the system
Taking the Laplace transforms of Equations 1 and 2 with assuming zero initial conditions, we get
\[{E_f}(s) = (s{L_f} + {R_f}){I_f}(s)…(3)\]
\[({s^2}J + sf)\theta (s) = {T_m}(s) = {{K’}_T}\hspace{0.1cm}{I_f}(s)….(4)\]
The transfer function of the system is obtained From Equations 3 and 4 as,
\[G(s) = \frac{{\theta (s)}}{{{E_f}(s)}} = \frac{{{K’}_T}}{{s[(s{L_f} + {R_f})(sJ + {f_o})]}}….(5)\]
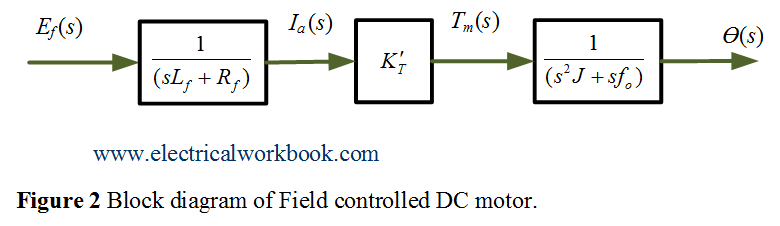
Block diagram of the system
The complete block diagram is obtained From Equations 3 and 4 as shown below in Figure 2.