After reading the MATLAB control systems topic, you will able to solve problems based on the control system in MATLAB, and you will also understand how to write transfer function, and how to find step response, impulse response of various transfer systems.
- It deals with control system design and analysis.
- It supports different transfer function and state-space forms.
- It provides in-built function to find step response, impulse response, parabolic response and ramp response of a dynamic system.
- It also provides in-built function for root locus, bode plot and Nyquist plot, and hence study the stability.
How to write transfer function?
The transfer function in the control system defined as the ratio of the Laplace transform of output to the Laplace transform of input, assuming all initial condition to be zero. The general form for writing transfer function is:
General Form:
sys = tf(num, den)
where,
- num is the vector of numerator coefficients in descending power of s.
- den is the vector of denominator coefficients in descending power of s.
- sys is an array which stores transfer function.
Example
Aim (1): To write given transfer function G(x) in MATLAB.
$G(s) = \frac{{2s + 12}}{{3{s^2} + 5s + 10}}$
Program (1):
num=[2 12]; den=[3 5 10]; sys = tf(num, den)Output (1):
sys = 2 s + 12 ---------------- 3 s^2 + 5 s + 10 Continuous-time transfer function.Step Response
Step response is the time response of a system when the system is subjected to step input. The general form for finding step response is:
General Form:
step(sys)where,
- sys is the name of defined transfer function.
Example
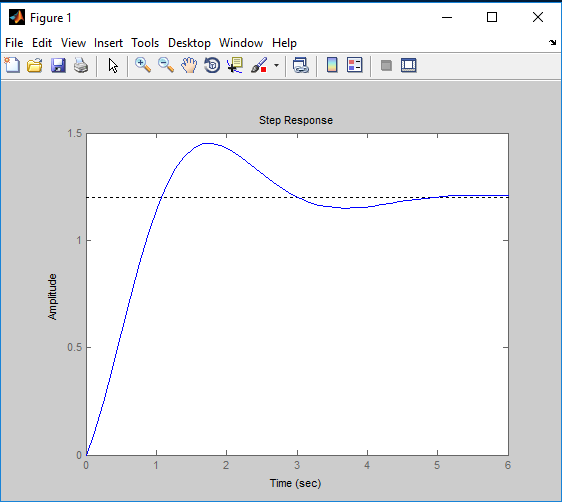
Aim (1): To find step response of given transfer function G(x) in MATLAB.
$G(s) = \frac{{2s + 12}}{{3{s^2} + 5s + 10}}$
Program (1):
num=[2 12]; den=[3 5 10]; sys = tf(num, den); step(sys)Output (1):
Impulse Response
Step response is the time response of a system when the system is subjected to impulse input. The general form for finding step response is:
General Form:
impulse(sys)where,
- sys is the name of the defined transfer function.
Example
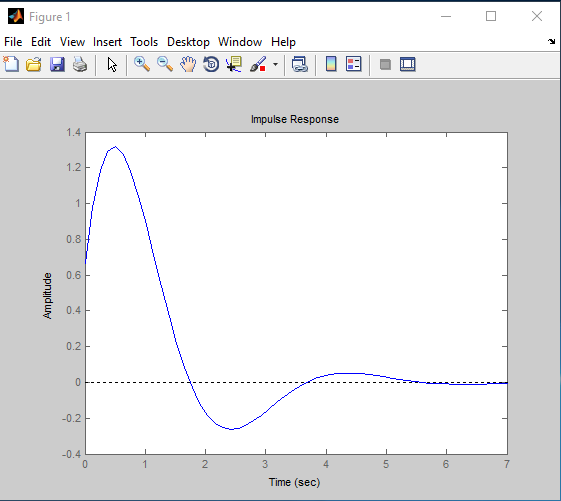
Aim (1): To find impulse response of given transfer function G(x) in MATLAB.
$G(s) = \frac{{2s + 12}}{{3{s^2} + 5s + 10}}$
Program (1):
num=[2 12]; den=[3 5 10]; sys = tf(num, den); impulse(sys)Output (1):
Root Locus
Root locus is the graphical representation of the poles of the closed-loop system when open loop transfer function is given. The general form for Root locus is:
General Form:
rlocus(sys)where,
- sys is the name of defined transfer function.
Example
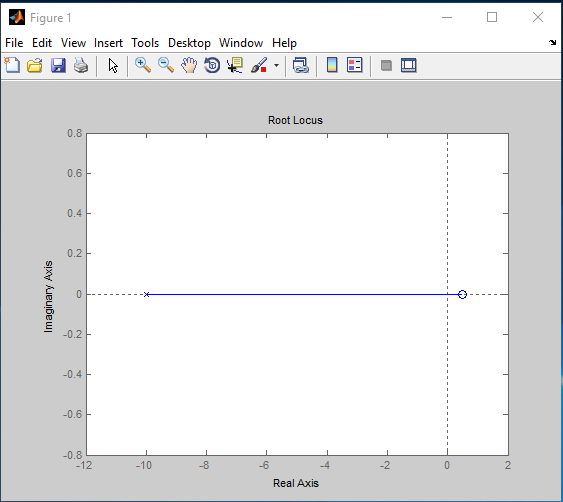
Aim (1): To find root locus of a given open transfer function G(x) in MATLAB.
$G(s) = \frac{{2s – 1}}{{s + 10}}$
Program (1):
num=[2 -1]; den=[1 10]; sys = tf(num, den); rlocus(sys)Output (1):