Compressors in which, air is trapped in a reduced space for compression by two sets of engaging surfaces is known as positive displacement compressors.
Vane Sealed Compressor
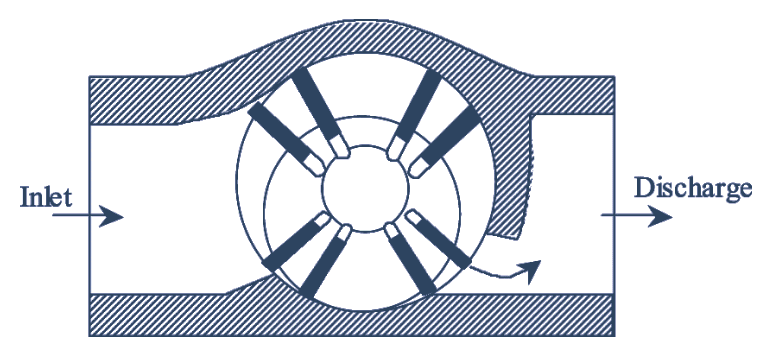
Figure 1: Vane Sealed Compressor.
The vanes are generally made of steel and sometimes of nonmetallic material such as fibre or carbon. Figure (1) shows a vane sealed compressor consisting of a rotor having slots mounted eccentrically in the body and vanes mounted on the rotor. During the rotation of rotor, the air from the inlet passage is drawn into the space between the rotor, the cylinder and two adjacent vanes. Further rotation of rotor causes the area between the rotor and the vanes to decrease and thereby resulting in compression of the air. As the rotor reaches the point just opposite to the eccentricity of the rotor, the suction ends and the compression proceeds and finally discharges the air through the discharge port. In this type of compressors, some or all of the compression is obtained before the air is delivered. It is also called as the sliding vane compressor. as the vanes slides in the rotor slots during its rotation. The vanes generally provided are 20 – 30 in number and as the number of vanes increases, the leakage losses decrease due to less pressure difference between the adjacent spaces. They are generally designed for the capacity upto 150 m3/min at a compression ratio upto 8.5. These compressors requires less work input compared to roots blower for the same pressure ratio and air delivery.

Figure 2: P-V Diagram for Vane Sealed Compressor.
The P-V diagram of a vane sealed compressor is shown in figure (2) below. From the figure, it is noticed that the air is compressed in the compressor upto a pressure of P and the remaining pressure rise occurs due to the back flow of air from the receiver.
Let, VS – induced volume at pressure P1 and temperature T1.
The workdone per revolution with N vanes is given by,
\[W=\frac{N\gamma }{\gamma -1}{{P}_{1}}{{V}_{1}}\left[ {{\left( \frac{{{P}_{i}}}{{{P}_{i}}} \right)}^{\frac{\gamma }{\gamma -1}}}-1 \right]+N({{P}_{2}}-{{P}_{i}}){{V}_{i}}\]