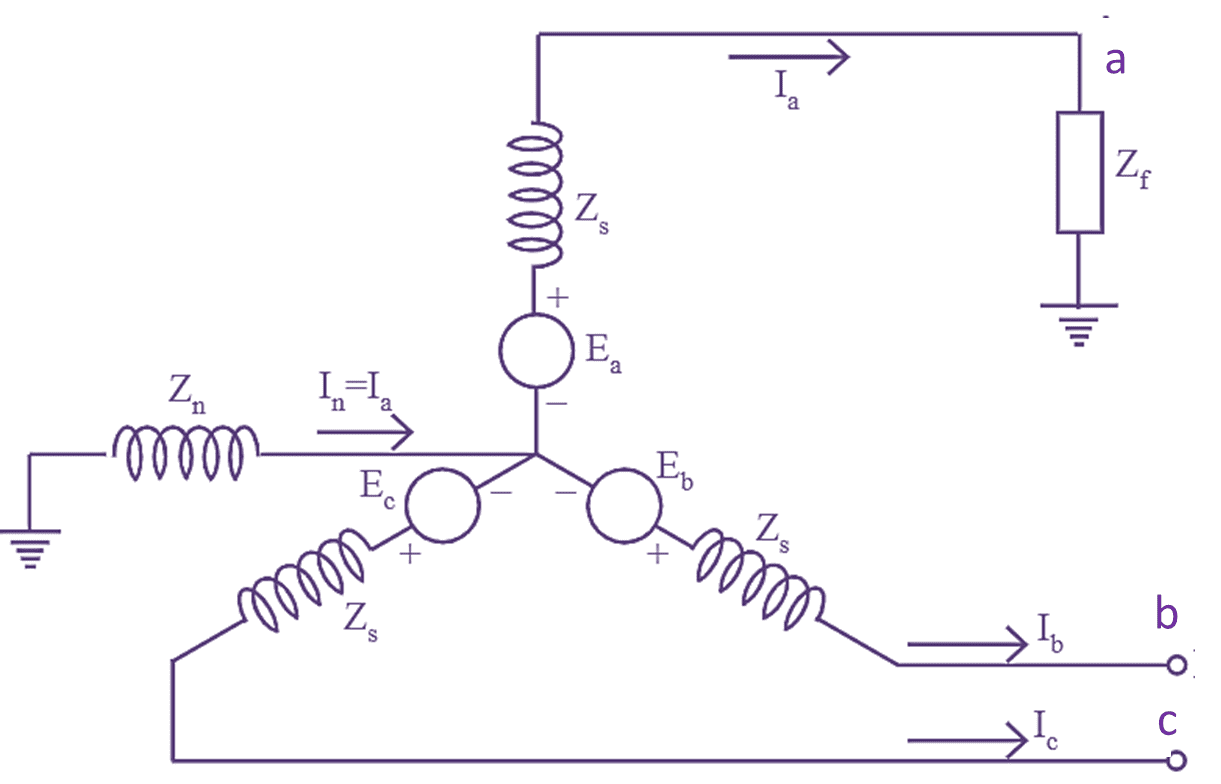
Figure 1: Single Line to Ground Fault.
Consider an unloaded 3-Φ generator with its neutral being grounded through an impedance Zn. Let a single line to ground fault occurs on phase ‘a’ through a fault impedance Zf as shown in figure (1). Under the fault condition the currents and voltage are given as
\[{{I}_{b}}={{I}_{c}}=0\]
\[{{V}_{a}}={{I}_{a}}{{Z}_{f}}…(1)\]
The symmetrical components of current are given as,
\[\left[ \begin{matrix}
{{I}_{a0}} \\
{{I}_{a1}} \\
{{I}_{a2}} \\
\end{matrix} \right]=\frac{1}{3}\left[ \begin{matrix}
1 & 1 & 1 \\
1 & a & {{a}^{2}} \\
1 & {{a}^{2}} & a \\
\end{matrix} \right]\left[ \begin{matrix}
{{I}_{a}} \\
{{I}_{b}} \\
{{I}_{c}} \\
\end{matrix} \right]\]
Substituting Ib = Ic = 0 in the above equation we get
\[\left[ \begin{matrix}
{{I}_{a0}} \\
{{I}_{a1}} \\
{{I}_{a2}} \\
\end{matrix} \right]=\frac{1}{3}\left[ \begin{matrix}
1 & 1 & 1 \\
1 & a & {{a}^{2}} \\
1 & {{a}^{2}} & a \\
\end{matrix} \right]\left[ \begin{matrix}
{{I}_{a}} \\
0 \\
0 \\
\end{matrix} \right]\]
\[=\frac{1}{3}\left[ \begin{matrix}
{{I}_{a}}+0+0 \\
{{I}_{a}}+0+0 \\
{{I}_{a}}+0+0 \\
\end{matrix} \right]=\frac{1}{3}\left[ \begin{matrix}
{{I}_{a}} \\
{{I}_{a}} \\
{{I}_{a}} \\
\end{matrix} \right]\]
\[{{I}_{a0}}={{I}_{a1}}={{I}_{a2}}=\frac{1}{3}{{I}_{a}}…(2)\]
For an unloaded 3-Φ generator we know that
\[{{V}_{a0}}=-{{I}_{a0}}{{Z}_{0}}\]
\[{{V}_{a1}}={{E}_{a}}-{{I}_{a1}}{{Z}_{1}}\]
\[{{V}_{a1}}=-{{I}_{a2}}{{Z}_{2}}\]
Also,
\[{{V}_{a}}={{V}_{a0}}+{{V}_{a1}}+{{V}_{a2}}\]
Substituting Va0, Va1 and Va2 in the above equation, we get
\[{{V}_{a}}=-{{I}_{a0}}{{Z}_{0}}-{{I}_{a1}}{{Z}_{1}}-{{I}_{a2}}{{Z}_{2}}\]
\[{{V}_{a}}={{E}_{a}}-\left( {{I}_{a0}}{{Z}_{0}}-{{I}_{a1}}{{Z}_{1}}-{{I}_{a2}}{{Z}_{2}} \right)\]
\[{{V}_{a}}={{E}_{a}}-\left( \frac{{{I}_{a}}}{3}{{Z}_{0}}+\frac{{{I}_{a}}}{3}{{Z}_{1}}+\frac{{{I}_{a}}}{3}{{Z}_{2}} \right)\]
\[{{V}_{a}}={{E}_{a}}-\frac{{{I}_{a}}}{3}\left( {{Z}_{0}}+{{Z}_{1}}+{{Z}_{2}} \right)…(3)\]
Substituting equation (1), in equation (3), we get
\[{{I}_{a}}{{Z}_{f}}={{E}_{a}}-\frac{{{I}_{a}}}{3}\left( {{Z}_{0}}+{{Z}_{1}}+{{Z}_{2}} \right)\]
\[3{{I}_{a}}{{Z}_{f}}=3{{E}_{a}}-{{I}_{a}}\left( {{Z}_{0}}+{{Z}_{1}}+{{Z}_{2}} \right)\]
\[3{{E}_{a}}=3{{I}_{a}}{{Z}_{f}}+{{I}_{a}}\left( {{Z}_{0}}+{{Z}_{1}}+{{Z}_{2}} \right)\]
\[3{{E}_{a}}={{I}_{a}}\left( {{Z}_{0}}+{{Z}_{1}}+{{Z}_{2}}+3{{Z}_{f}} \right)\]
\[{{I}_{a}}=\frac{3{{E}_{a}}}{{{Z}_{0}}+{{Z}_{1}}+{{Z}_{2}}+3{{Z}_{f}}}\]
From equation (2), we have
\[{{I}_{a0}}={{I}_{a1}}={{I}_{a2}}=\frac{1}{3}{{I}_{a}}\]
\[=\frac{1}{3}\left( \frac{3{{E}_{a}}}{{{Z}_{0}}+{{Z}_{1}}+{{Z}_{2}}+3{{Z}_{f}}} \right)\]
\[=\frac{{{E}_{a}}}{{{Z}_{0}}+{{Z}_{1}}+{{Z}_{2}}+3{{Z}_{f}}}\]
The fault current is,
\[{{I}_{f}}={{I}_{a}}=\frac{3{{E}_{a}}}{{{Z}_{0}}+{{Z}_{1}}+{{Z}_{2}}+3{{Z}_{f}}}\]
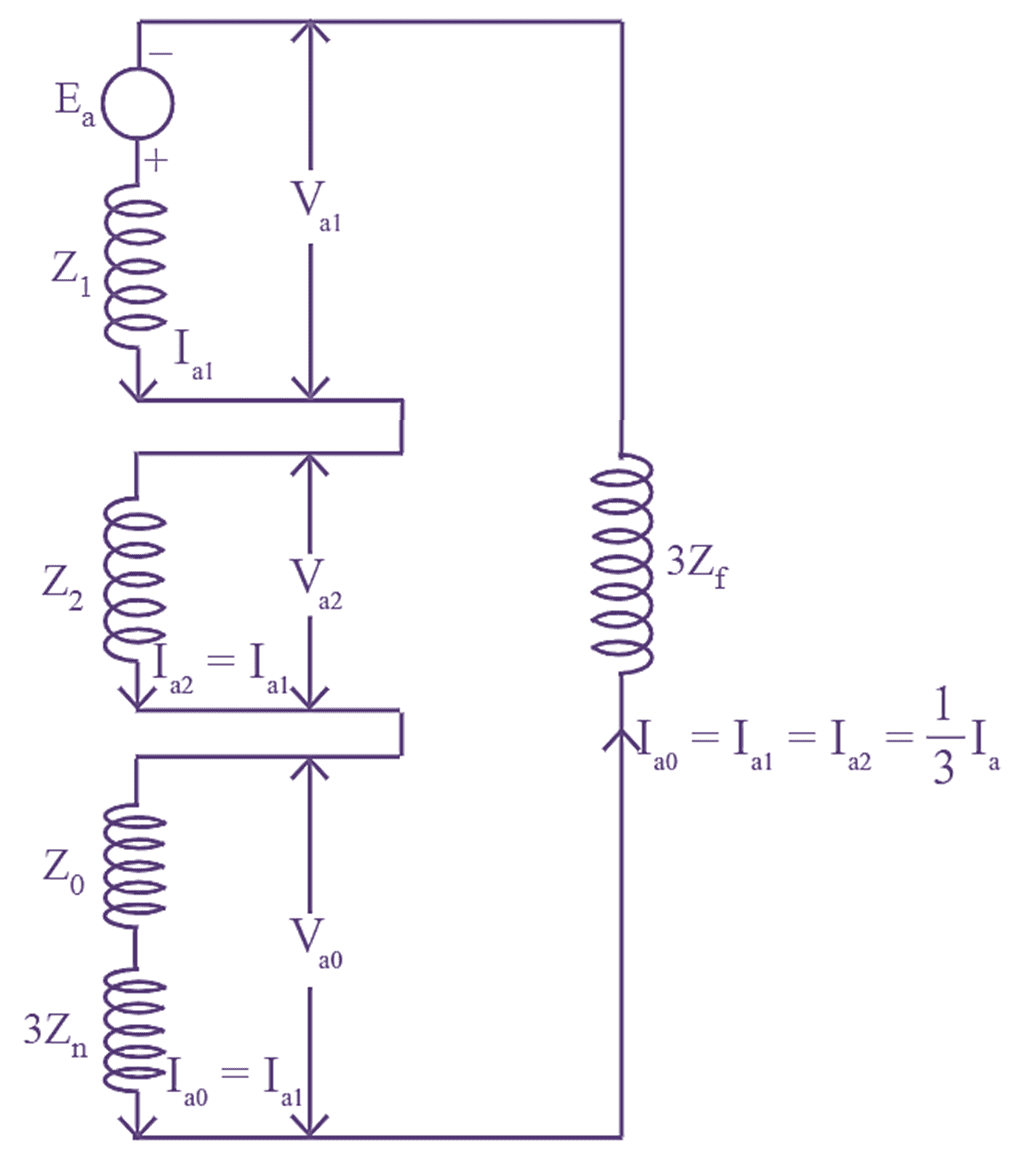
Figure 2: Interconnection of sequence Network of Single Line to Ground Fault.
Hence, from the above equation it is observed that, inter connection of sequence networks to simulate L-G fault contains positive, negative and zero sequence networks. As the three sequence networks carry the same current they are connected in series as shown in figure (2). If an alternator neutral is solidly grounded, Zn = 0.