After reading this topic Steady state error in the control system, you will understand the theory, expression, derivation, factors, and block diagram.
Steady state error defined as the difference between the input signal and the output signal in a steady state. It depends on the type of system and type of the input signal.
How to determine steady-state error
Consider a simple closed loop control system with negative feedback as shown below in Figure 1.
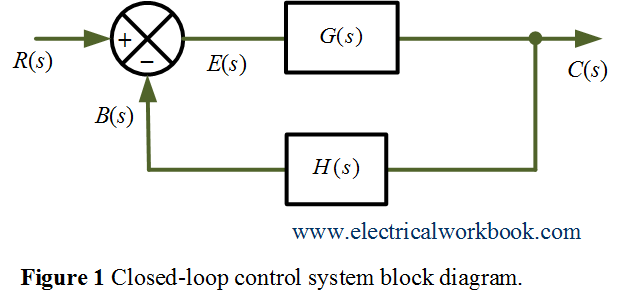
where R(s) is the input signal, B(s) is the feedback signal, C(s) is the output signal, G(s) is the forward gain, H(s) is the feedback gain and error signal E(s) is the difference between input R(s) and feedback signal B(s).
From the Figure 1,
\[E(s) = R(s) – B(s)….(1)\]
also,
\[B(s) = C(s)H(s)….(2)\]
\[C(s) = E(s)G(s)…..(3)\]
Using Equations 1,2 and 3 gives
\[E(s) = R(s) – C(s)H(s)\]
\[ = R(s) – E(s)G(s)H(s)\]
\[E(s) = \frac{{R(s)}}{{1 + G(s)H(s)}}……(4)\]
Steady – state error is given as,
\[{e_{ss}} = \mathop {\lim }\limits_{t \to \infty } e(t)\]
Using final value theorem,
\[{e_{ss}} = \mathop {\lim }\limits_{s \to 0} sE(s)….(5)\]
From Equation 4 and Equation 5 gives,
\[{e_{ss}} = \mathop {\lim }\limits_{s \to 0} \frac{{sR(s)}}{{1 + G(s)H(s)}}…..(6)\]
Factors on which steady-state error depends
From Equation 6 we can coclude that steady-state error depends on the following factors.
- Input signal R(s)
- Open-loop transfer function G(s)H(s) or type the system.