In this topic, you study Torque Slip Characteristics of Induction Motor.
As the rotor of an induction motor speeds up from rest after starting, the slip and therefore rotor emf, frequency and reactance gradually decrease. Consequently, the rotor current is decreased and the rotor power factor is improved. Initially, the increase in rotor power factor causes the torque to increase. But in the later stages, when the reactance becomes very small, the effect of the decrease in rotor current predominates. Hence, the torque decreases rapidly and finally becomes zero at synchronous speed. If the torque (T) is plotted against the slip (S) from S = 1 (standstill condition) to S = 0 (synchronous speed condition), we get the curve known as torque slip characteristic of an induction motor. This curve is very important as it reveals lot of information with regard to the behaviour of the motor. Fig. 1(a) shows one such typical curve. The nature of the curve can be very well explained from the torque equation as follows:
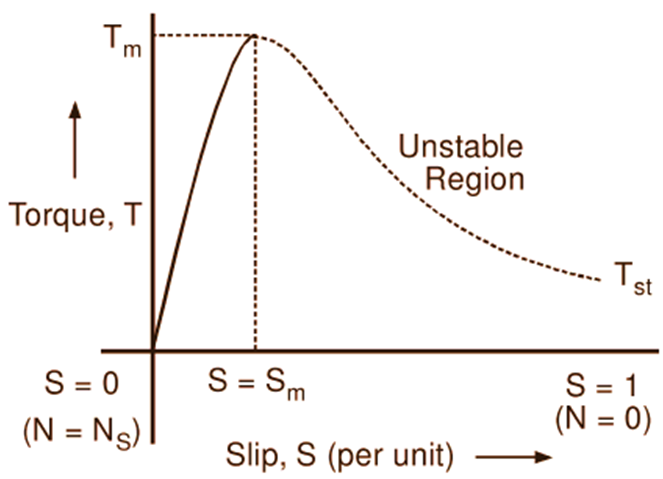
Fig. 1: Torque slip characteristics of an induction motor
For a given supply voltage, flux per Stator pole (Φ) and hence the standstill rotor emf per phase (E2) being constant,
\[\text{T}\propto \frac{\text{S}{{\text{R}}_{\text{2}}}}{\text{R}_{\text{2}}^{\text{2}}\text{+(S}{{\text{X}}_{\text{2}}}{{\text{)}}^{\text{2}}}}….(1)\]
From the above equation, it is evident that when S = 0 (at synchronous speed), T = 0. Hence the torque slip curve Starts from the origin (0, 0). For small values of slip (at normal speeds close to synchronism), the term ${{\text{(S}{{\text{X}}_{\text{2}}}\text{)}}^{\text{2}}}$ in the denominator of the Equation 1 is very small in comparison with the term $\text{R}_{\text{2}}^{\text{2}}$ and hence can be neglected. In such a case,
\[\text{T}\propto \frac{\text{S}}{{{\text{R}}_{\text{2}}}}\propto \text{S}….(2)\]
(if R2 is constant)
Thus, for small values of slip, the torque is directly proportional to the slip and hence the torque slip curve is a straight line. As the slip increases with the increase in the load on the motor, the torque increases. It becomes maximum when $\text{S}={{\text{S}}_{\text{m}}}={{\text{R}}_{\text{2}}}/{{\text{X}}_{\text{2}}}$. This torque is known as pull-out or break-down torque. For higher values of slip (resulting from further increase in the motor load), the term $\text{R}_{\text{2}}^{\text{2}}$ in the denominator of the torque expression becomes negligible in comparison with the term ${{\text{(S}{{\text{X}}_{\text{2}}}\text{)}}^{\text{2}}}$.
\[\text{T}\propto \frac{{{\text{R}}_{\text{2}}}}{\text{SX}_{2}^{2}}\propto \frac{\text{1}}{\text{S}}….(3)\]
(if R2 and X2 are constant)
So, for higher values of slip (beyond the value that corresponds to maximum torque), the torque is inversely proportional to the slip and the torque-slip curve is a rectangular hyperbola as shown in the figure.
Thus, it will be seen that when the load on the motor is increased, the slip increases and therefore the torque increases until it attains the maximum value. However, any further increase in the motor load results in decrease of torque developed by the motor. As a result, the motor slows down and eventually stops. Hence, the dotted portion of the curve represents unstable conditions. It should be noted that the torque can also be plotted against the rotor speed as illustrated in Fig. 2.
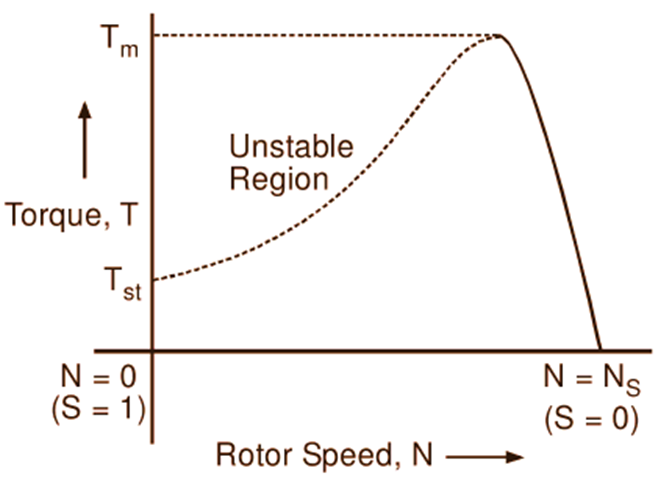
Fig. 2: Torque-speed characteristics of an induction motor
Effect of Rotor Resistance on Torque Slip Characteristic
The value of the maximum torque is independent of the rotor resistance. Further, from Expression (3), it will be seen that with high values of slip i.e. when the rotor resistance R2 is small compared with the rotor reactance SX2, the torque of the motor for a given slip is directly proportional to the value of the rotor resistance. On the other hand, Expression (2) shows that with small values of slip i.e. when the rotor resistance R2 is large compared with the rotor reactance SX2, the torque of the motor for a given slip is inversely proportional to the value of the rotor resistance. Fig. 3 shows the torque slip curves for different values of rotor resistance. The effect of the rotor resistance on the shape of the torque slip curve can be very well seen from these curves. If a large starting torque is required, the rotor must have a relatively high resistance. If it is made sufficiently large (with R2 = X2), maximum torque may be obtained at starting itself. However, with such a high rotor resistance, slip for full-load torque would be very large.
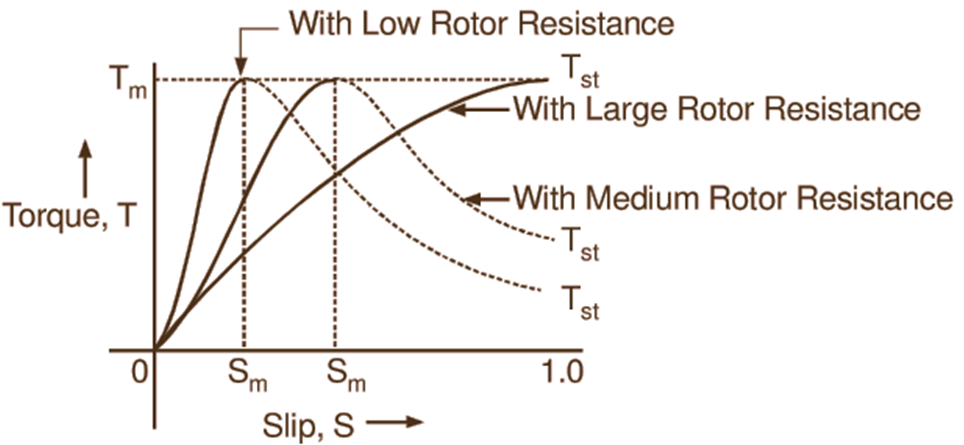
Fig. 3: Effect of rotor resistance on torque slip characteristic Of an induction motor.
The copper loss (i.e. I2R loss) in the rotor winding would be high and therefore temperature rise would be excessive. Also the efficiency and speed of the motor would be poor. In practice, when a motor is required to exert its maximum torque at starting, initially the extra resistance is inserted into the rotor circuit and subsequently this resistance is gradually cut out as the motor accelerates. Thus good performance under starting as well as running conditions becomes possible. Such an arrangement is possible only with wound rotors. The motors with low resistance cage type rotors, therefore, have inherently low starting torque.