In this topic, you study Current Divider Rule – Derivation, Formula & Theory.
According to Current divider Rule, the division of current in the two branches of a parallel circuit is inversely proportional to their resistances.
When a number of resistances are connected in parallel, current in each branch is different from the other. Fig. 1 (a) shows a parallel circuit consisting of two resistances R1 and R2 connected in parallel across a source of potential difference V volts and drawing total current of I amperes.
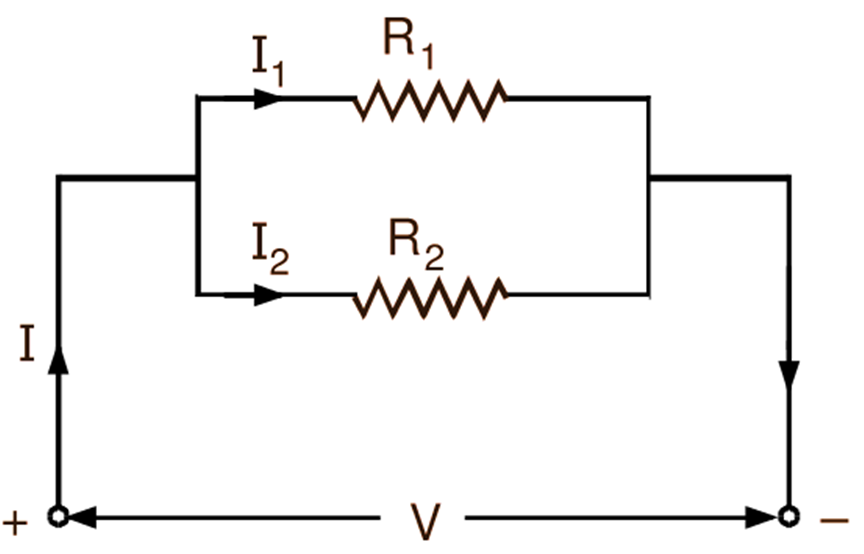
Fig. 1: Resistances in parallel
Let I1 and I2 be the currents in the resistances R1 and R2 respectively. Applying Ohm’s law to both branches of this circuit, we have
\[{{\text{I}}_{1}}=\frac{\text{V}}{{{\text{R}}_{1}}}\]
and
\[{{\text{I}}_{2}}=\frac{\text{V}}{{{\text{R}}_{2}}}\]
Thus,
\[\frac{{{\text{I}}_{1}}}{{{\text{I}}_{2}}}=\frac{{{\text{R}}_{2}}}{{{\text{R}}_{1}}}\]
Hence, the division of current in the two branches of a parallel circuit is inversely proportional to their resistances.
The current in any branch of the parallel circuit can also be expressed in terms of total current drawn by the circuit. Here,
\[\text{V}=\text{IR}={{\text{I}}_{1}}{{\text{R}}_{1}}={{\text{I}}_{2}}{{\text{R}}_{2}}\]
Hence,
\[{{\text{I}}_{1}}=\text{I}\times \frac{\text{R}}{{{\text{R}}_{1}}}\]
But, Equivalent resistance,
\[\frac{\text{1}}{\text{R}}=\frac{\text{1}}{{{\text{R}}_{1}}}+\frac{\text{1}}{{{\text{R}}_{2}}}\]
\[\text{R}=\frac{{{\text{R}}_{1}}{{\text{R}}_{2}}}{{{\text{R}}_{1}}+{{\text{R}}_{2}}}\]
Thus,
\[{{\text{I}}_{1}}=\text{I}\times \frac{{{\text{R}}_{2}}}{{{\text{R}}_{1}}+{{\text{R}}_{2}}}\]
Similarly,
\[{{\text{I}}_{2}}=\text{I}\times \frac{{{\text{R}}_{1}}}{{{\text{R}}_{1}}+{{\text{R}}_{2}}}\]
The above results can be extended for a parallel circuit consisting of three branches in parallel shown in Fig. 2. Here,
\[\text{V}=\text{IR}={{\text{I}}_{1}}{{\text{R}}_{1}}={{\text{I}}_{2}}{{\text{R}}_{2}}={{\text{I}}_{3}}{{\text{R}}_{3}}\]
Hence,
\[{{\text{I}}_{1}}=\text{I}\times \frac{\text{R}}{{{\text{R}}_{1}}}\]
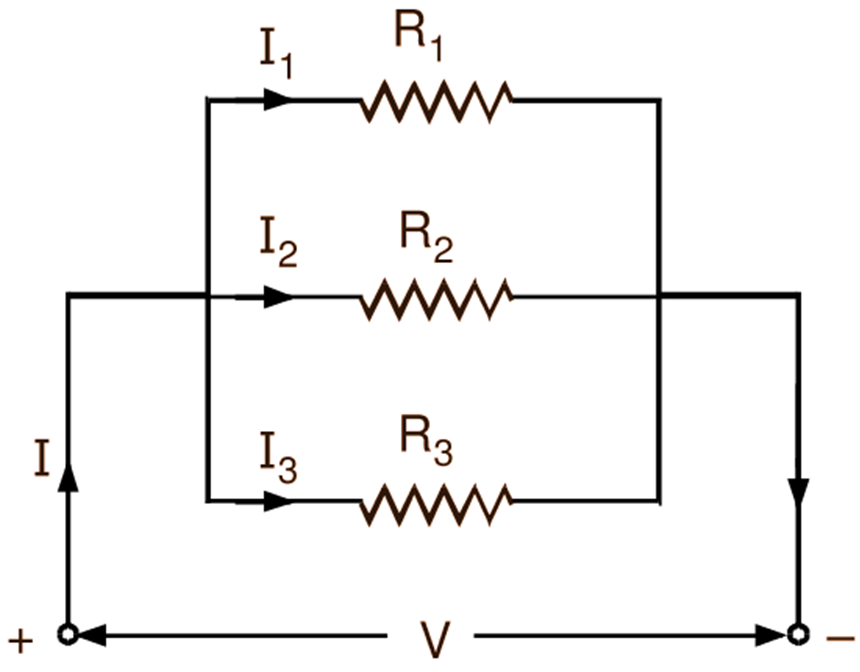
Fig. 2: Resistances in parallel
But, Equivalent resistance,
\[\frac{\text{1}}{\text{R}}=\frac{\text{1}}{{{\text{R}}_{1}}}+\frac{\text{1}}{{{\text{R}}_{2}}}+\frac{\text{1}}{{{\text{R}}_{3}}}\]
Also,
\[\text{R}=\frac{{{\text{R}}_{1}}{{\text{R}}_{2}}{{\text{R}}_{3}}}{{{\text{R}}_{1}}{{\text{R}}_{2}}+{{\text{R}}_{2}}{{\text{R}}_{3}}+{{\text{R}}_{3}}{{\text{R}}_{1}}}\]
Thus,
\[{{\text{I}}_{1}}=\text{I}\times \frac{{{\text{R}}_{2}}{{\text{R}}_{3}}}{{{\text{R}}_{1}}{{\text{R}}_{2}}+{{\text{R}}_{2}}{{\text{R}}_{3}}+{{\text{R}}_{3}}{{\text{R}}_{1}}}\]
Similarly,
\[{{\text{I}}_{2}}=\text{I}\times \frac{{{\text{R}}_{3}}{{\text{R}}_{1}}}{{{\text{R}}_{1}}{{\text{R}}_{2}}+{{\text{R}}_{2}}{{\text{R}}_{3}}+{{\text{R}}_{3}}{{\text{R}}_{1}}}\]
\[{{\text{I}}_{3}}=\text{I}\times \frac{{{\text{R}}_{3}}{{\text{R}}_{1}}}{{{\text{R}}_{1}}{{\text{R}}_{2}}+{{\text{R}}_{2}}{{\text{R}}_{3}}+{{\text{R}}_{3}}{{\text{R}}_{1}}}\]