In this topic, you study Capacitors in Series – Derivation, Formula & Theory.
Consider three capacitors of capacitances C1, C2, and C3 farads respectively connected in series across a d.c. supply of V volts, through a switch Sw, as illustrated in Fig. 1. When the switch Sw is closed, all these capacitors are charged. Since there is similar displacement of electrons through each capacitor, they acquire equal charges.
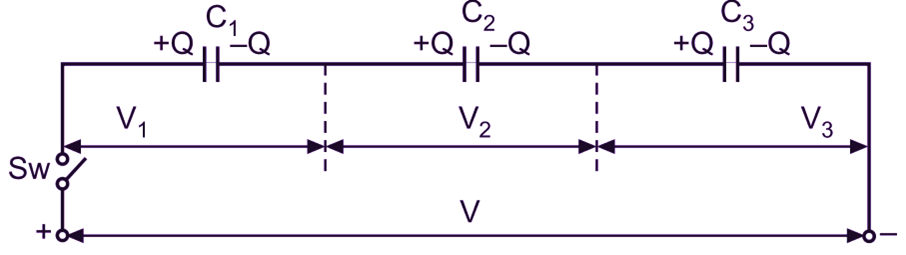
Fig. 1: Capacitors in series.
Let the charges each be Q coulombs. Also, let V1, V2, and V3 be the potential differences established across the capacitors with capacitances C1, C2, and C3 respectively, in their fully charged condition. Then,
\[{{\text{V}}_{\text{1}}}=\text{ }\frac{\text{Q}}{{{\text{C}}_{\text{1}}}}\]
\[{{\text{V}}_{\text{2}}}=\text{ }\frac{\text{Q}}{{{\text{C}}_{\text{2}}}}\]
and
\[{{\text{V}}_{\text{3}}}=\text{ }\frac{\text{Q}}{{{\text{C}}_{\text{3}}}}\]
Now, by the application of Kirchhoff’s voltage law to the circuit (Fig. 1), it follows that the sum of three capacitor voltages must be equal to the total applied voltage i.e.
\[\text{V}=\text{ }{{\text{V}}_{\text{1}}}\text{+ }{{\text{V}}_{\text{2}}}\text{ + }{{\text{V}}_{\text{3}}}\]
also
\[\text{V}=\text{ }\frac{\text{Q}}{{{\text{C}}_{\text{1}}}}\text{+ }\frac{\text{Q}}{{{\text{C}}_{\text{2}}}}\text{ + }\frac{\text{Q}}{{{\text{C}}_{\text{3}}}} ….(1)\]
But, if C is the capacitance of an equivalent single capacitor for the three given capacitors in series, acquiring the same charge of Q coulombs, when the same voltage of V volts is applied across its terminals, then
\[\text{V}=\text{ }\frac{\text{Q}}{\text{C}} ….(2)\]
Hence, from Equation (1) and Equation (2),
\[\frac{\text{Q}}{\text{C}}=\text{ }\frac{\text{Q}}{{{\text{C}}_{\text{1}}}}\text{+ }\frac{\text{Q}}{{{\text{C}}_{\text{2}}}}\text{ + }\frac{\text{Q}}{{{\text{C}}_{\text{3}}}}\]
∴
\[\frac{\text{1}}{\text{C}}=\text{ }\frac{\text{1}}{{{\text{C}}_{\text{1}}}}\text{+ }\frac{\text{1}}{{{\text{C}}_{\text{2}}}}\text{ + }\frac{\text{1}}{{{\text{C}}_{\text{3}}}}\]
In general, if the number of capacitors connected in series is n, then
\[\frac{\text{1}}{\text{C}}=\text{ }\frac{\text{1}}{{{\text{C}}_{\text{1}}}}\text{+ }\frac{\text{1}}{{{\text{C}}_{\text{2}}}}\text{ + }\frac{\text{1}}{{{\text{C}}_{\text{3}}}}+….+\frac{\text{1}}{{{\text{C}}_{\text{n}}}}\]
The various results obtained in respect of a series combination of capacitors can be summarized as below:
(i) All the capacitors connected in series acquire equal charges.
(ii) The supply voltage (V) is always equal to the sum of the potential differences established across the capacitors i.e.
\[\text{V}=\text{ }{{\text{V}}_{\text{1}}}\text{+ }{{\text{V}}_{\text{2}}}\text{ + }{{\text{V}}_{\text{3}}}\]
(iii) The reciprocal of the equivalent capacitance of a number of capacitors connected in series is equal to the Sum Of the reciprocals of the capacitances of the individual capacitors i.e.
\[\frac{\text{1}}{\text{C}}=\text{ }\frac{\text{1}}{{{\text{C}}_{\text{1}}}}\text{+ }\frac{\text{1}}{{{\text{C}}_{\text{2}}}}\text{ + }\frac{\text{1}}{{{\text{C}}_{\text{3}}}}+….+\frac{\text{1}}{{{\text{C}}_{\text{n}}}}\]