Coefficient of Coupling

In this topic, you study Coefficient of Coupling.

As the two coils A and C shown in Fig. 1 are brought close together, all the flux Φ₁ produced by current I₁ in coil A does not link coil C. Only a fraction K₁ of this flux i.e. K₁Φ₁ (where K₁ < 1) links with coil C.

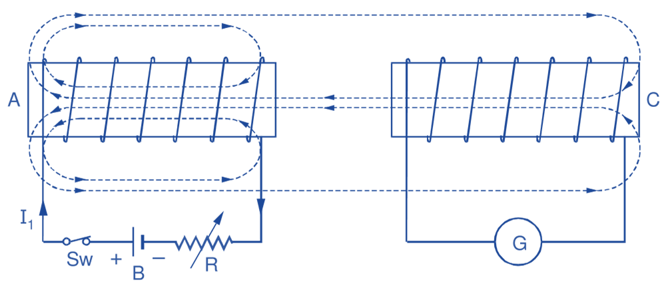
Fig. 1: Mutual induction

Thus the Equation for the coefficient of mutual induction under this condition is given by

\[\text{M}=\frac{{{\text{N}}_{\text{2}}}{{\text{K}}_{\text{1}}}{{\phi }_{\text{1}}}}{{{\text{I}}_{\text{1}}}}….(1)\]

Similarly, if the current I₂ flowing in coil C produces flux Φ₂ and the fraction K₂ of this flux i.e. K₂Φ₂ (where K₂ < 1) links with coil A, then the coefficient of mutual induction is also given by

\[\text{M}=\frac{{{\text{N}}_{\text{1}}}{{\text{K}}_{\text{2}}}{{\phi }_{\text{2}}}}{{{\text{I}}_{\text{2}}}}….(1)\]

Multiplying Equation (1) by Equation (2), we get

\[{{\text{M}}^{2}}={{\text{K}}_{\text{1}}}{{\text{K}}_{\text{2}}}\times \frac{{{\text{N}}_{\text{1}}}{{\phi }_{\text{1}}}}{{{\text{I}}_{\text{1}}}}\times \frac{{{\text{N}}_{\text{2}}}{{\phi }_{\text{2}}}}{{{\text{I}}_{\text{2}}}}\]

\[{{\text{M}}^{2}}={{\text{K}}_{\text{1}}}{{\text{K}}_{\text{2}}}{{\text{L}}_{\text{1}}}{{\text{L}}_{\text{2}}}\]

\[\text{since, L}=\frac{\text{N}\phi }{\text{I}}\]

where L₁ and L₂ are the coefficients of self induction of the coils A and C respectively.

\[\text{M}=\text{K}\sqrt{{{\text{L}}_{\text{1}}}{{\text{L}}_{\text{2}}}}\]

or,

\[\text{K}=\frac{\text{M}}{\sqrt{{{\text{L}}_{\text{1}}}{{\text{L}}_{\text{2}}}}}\]

where $\text{K}=\sqrt{{{\text{K}}_{\text{1}}}{{\text{K}}_{\text{2}}}}$

The constant K in the above expression is called the coefficient of coupling. If the flux due to one coil completely links with the other coil, then K₁ = K₂ = K = 1. Under this condition, the mutual inductance between the two coils is maximum and given by

\[\text{M}=\sqrt{{{\text{L}}_{\text{1}}}{{\text{L}}_{\text{2}}}}\]

Therefore,

The coefficient of coupling of the coils A and C can be defined as the ratio of the actual mutual inductance present between the two coils to its maximum possible value.

It should be noted that if K₁ = K₂ as is the usual case, then Co-efficient of coupling,

K = K₁ = K₂

When the flux due to one coil completely links with the other coil i.e. when K = 1, the coils are said to be tightly coupled, on the other hand, when only a small fraction of the flux of one coil links with the other, the coils are said to be loosely coupled.