After reading this topic Settling time $({t_s})$ in Time response of a second-order control system for subjected to a unit step input underdamped case, you will understand the theory, expression, and plot.
A block diagram of the second order closed-loop control system with unity negative feedback is shown below in Figure 1,
The general expression for the time response of a second order control system or underdamped case is
\[c(t) = 1 – \frac{{{e^{ – \xi {\omega _n}t}}}}{{\sqrt {1 – {\xi ^2}} }}\sin \left[ {({\omega _n}\sqrt {1 – {\xi ^2}} )t + \theta } \right]…(1)\]
Also Equation 1, is plotted in Figure 2 as shown below
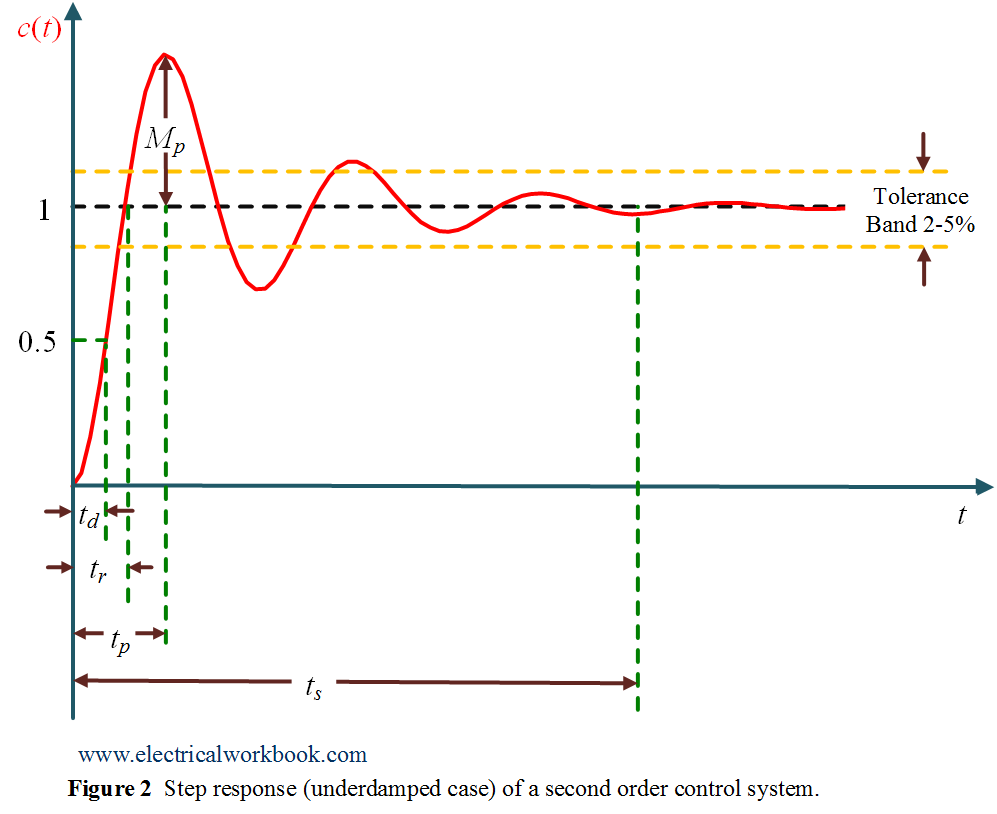
Settling time $(t_s)$
In second order underdamped control system when unity step input applied, oscillation in the response occurs initially in the output time response and the magnitude of the oscillations decay exponentially with time constant $ 1/(\xi {\omega _n})$ . Settling time is the time taken by the response to settle down oscillations and stay within 2% or 5% error (or tolerance) band of its final value. Its general expression as
For 2% error (or tolerance) band,
\[{t_s} = \frac{4}{{\xi {\omega _n}}}\]
For 5% error (or tolerance) band,
\[{t_s} = \frac{3}{{\xi {\omega _n}}}\]
