What is Anderson Bridge? Theory, Diagram, Derivation & Advantages

Anderson bridge is used to measure inductance in terms of a standard capacitance (C). This method is applicable for precise measurement of inductance over a wide range of values, from micro henry to several henries. The Fig. 1. shows the circuit diagram of the bridge. The circuit has the following components.

L₁ = Inductance to be measured

R₁ = Resistance of the inductor

r₁ = Resistance connected in series with L₁

r, R₂, R₃, R₄ = Known non-inductive resistors

C = Fixed standard capacitor.

.

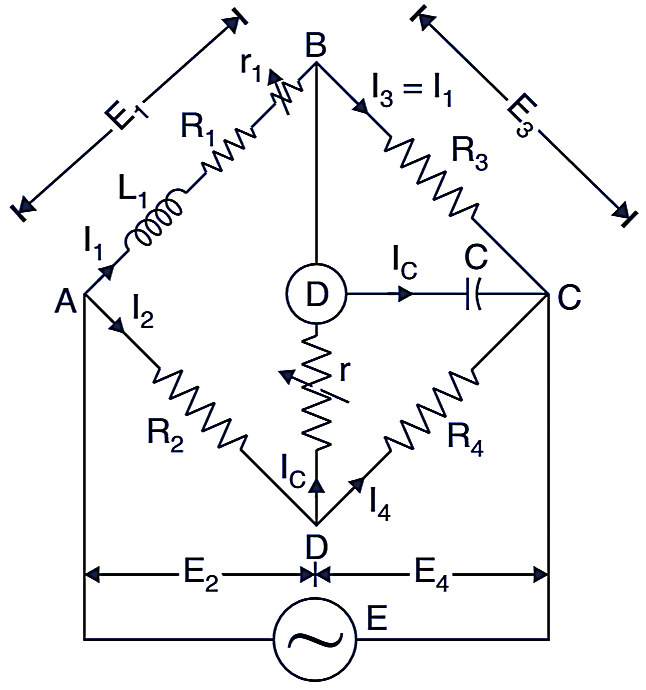
Fig. 1. Anderson bridge

Balance is obtained by varying (adjusting) the resistance r₁ and r.

At balance,

\[{{\text{I}}_{\text{1}}}\text{ =  }{{\text{I}}_{\text{3}}}\]

and

\[{{\text{I}}_{\text{C}}}\left( \text{r +}\frac{1}{\text{j}\omega \text{C}} \right)=\left( {{\text{I}}_{\text{2}}}-\text{ }{{\text{I}}_{\text{C}}} \right){{\text{R}}_{\text{4}}}\]

Now.

\[{{\text{I}}_{\text{1}}}{{\text{R}}_{\text{3}}}\text{ =  }{{\text{I}}_{\text{C}}}\times \frac{1}{\text{j}\omega \text{C}}\]

i.e.

\[{{\text{I}}_{\text{C}}}\text{ =  }{{\text{I}}_{\text{1}}}{{\text{R}}_{\text{3}}}\text{ j}\omega \text{C}\]

Writing balance equations

\[{{\text{I}}_{\text{1}}}\left( {{\text{R}}_{\text{1}}}\text{+ }{{\text{r}}_{\text{1}}}\text{+ j}\omega {{\text{L}}_{\text{1}}} \right)\text{ =  }{{\text{I}}_{\text{2}}}{{\text{R}}_{\text{2}}}\text{+ }{{\text{I}}_{\text{C}}}\text{ r}…(i)\]

and

\[{{\text{I}}_{\text{C}}}\left( \text{r +}\frac{1}{\text{j}\omega \text{C}} \right)=\left( {{\text{I}}_{\text{2}}}-{{\text{I}}_{\text{C}}} \right){{\text{R}}_{\text{4}}}\]

Putting the value of I_C the eq. (1) can be written as:

\[{{\text{I}}_{\text{C}}}\left( {{\text{R}}_{\text{1}}}\text{+ }{{\text{r}}_{\text{1}}}\text{+ j}\omega {{\text{L}}_{\text{1}}} \right)\text{ =  }{{\text{I}}_{\text{2}}}{{\text{R}}_{\text{2}}}\text{+ }{{\text{I}}_{\text{C}}}\text{ r}\]

or,

\[{{\text{I}}_{\text{1}}}\left( {{\text{R}}_{\text{1}}}\text{+ }{{\text{r}}_{\text{1}}}\text{+ j}\omega {{\text{L}}_{\text{1}}}-{{\text{R}}_{\text{3}}}\text{ j}\omega \text{C r} \right)\text{ =  }{{\text{I}}_{\text{2}}}{{\text{R}}_{\text{2}}}…(iii)\]

Now putting the value of I_C the eq. (ii) can be written as:

\[{{\text{I}}_{\text{1}}}{{\text{R}}_{\text{3}}}\text{ j}\omega \text{C}\left( \text{r +}\frac{1}{\text{j}\omega \text{C}} \right)=\left( {{\text{I}}_{\text{2}}}-\text{ }{{\text{I}}_{\text{1}}}{{\text{R}}_{\text{3}}}\text{ j}\omega \text{C} \right){{\text{R}}_{\text{4}}}\]

or,

\[{{\text{I}}_{\text{1}}}\left( \text{j}\omega \text{C }{{\text{R}}_{\text{3}}}\text{ r}+\text{j}\omega \text{C }{{\text{R}}_{\text{3}}}{{\text{R}}_{\text{4}}}\text{+ }{{\text{R}}_{\text{3}}} \right)\text{ =  }{{\text{I}}_{\text{2}}}{{\text{R}}_{\text{4}}}…(iv)\]

From eq. (iii) and (iv) we get

${{\text{I}}_{\text{1}}}\left( {{\text{R}}_{\text{1}}}\text{+ }{{\text{r}}_{\text{1}}}\text{+ j}\omega {{\text{L}}_{\text{1}}}-{{\text{R}}_{\text{3}}}\text{ j}\omega \text{C r} \right)\text{ }$

\[\text{=  }\left[ \frac{{{\text{R}}_{\text{2}}}{{\text{R}}_{\text{3}}}}{{{\text{R}}_{\text{4}}}}+\frac{\text{j}\omega \text{C }{{\text{R}}_{\text{2}}}{{\text{R}}_{\text{3}}}\text{ r}}{{{\text{R}}_{\text{4}}}}+\text{j}\omega \text{C }{{\text{R}}_{\text{2}}}{{\text{R}}_{\text{3}}} \right]\]

Equating real and imaginary tenus,

\[{{\text{R}}_{\text{1}}}\text{ = }\frac{{{\text{R}}_{\text{2}}}{{\text{R}}_{\text{3}}}}{{{\text{R}}_{\text{4}}}}\]

.\[{{\text{L}}_{\text{1}}}\text{ = C}\frac{{{\text{R}}_{\text{3}}}}{{{\text{R}}_{\text{4}}}}\left[ \text{r}\left( {{\text{R}}_{\text{4}}}\text{+ }{{\text{R}}_{\text{2}}} \right)+{{\text{R}}_{\text{2}}}{{\text{R}}_{\text{4}}} \right]\]

Advantages of Anderson Bridge

1. The adjustments are carried out by manipulating R₁ and r and they become independent of each other. This is a superior point. It is easy to obtain balance in this bridge as compared to Maxwell Bridge.
2. A fixed capacitor can be used instead of a variable capacitor.
3. This bridge may also be used to measure capacitance in terms of inductance.

Disadvantages of Anderson Bridge

1. The Anderson’s bridge is very complex as compared to Maxwell Bridge. It has a circuit with more components. The balance equations are also very tedious.
2. Due to above reason, Maxwell bridge is preferred.