Manometer is an important device for measuring flow and pressure differences. Three different manometers which are commonly used have been discussed below.
Simple Manometer
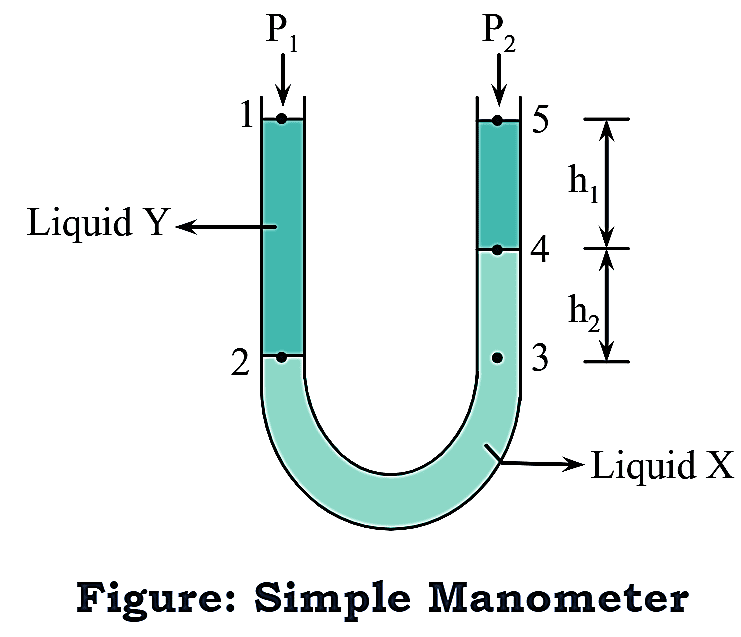
Simple manometer is most commonly used for measuring the pressure difference. It consists of U-shaped glass tube which is filled with liquid X and Y. X and Y are the two immiscible liquids the light shaded portion of the tube is filled with liquid X having a density ‘ρX‘. The arms of the tube above the liquid X i.e., the dark shaded portion is filled with liquid Y having density ‘ρy‘. The pressure exerted in left arm of the tube at point 1 is P1 (pascals). Similarly, pressure P2 is exerted in right arm of the tube at point 5.
According to fluid statics, the pressure at point 2 is given by the equation below.
1. At point 2, the pressure is = P1 + (h1 + h2)ρyg ….(1)
Where, (h1 + h2) Distance from 3 to 5.
2. At point 3, the pressure is = P1 + (h1 + h2) ρyg ….(2)
[2, 3 are at the same level]
3. At point 4, the pressure is = P2 + h1ρyg ….(3)
Equation (3) is written by considering the right arm of the tube.
The pressure at point 4 can also be “written by considering the left arm of the tube as follows,
At point 4, the pressure is = P1 + ρY (h1 + h2)g ρxh2g ….(4)
Equations (3) and (4) are equated because both the equations represent the pressure at point 4. Hence,
\[{{P}_{1}}+{{\rho }_{Y}}({{h}_{1}}+{{h}_{2}})g-{{\rho }_{X}}{{h}_{2}}g={{P}_{2}}+{{h}_{1}}{{\rho }_{y}}g\]
\[{{P}_{1}}-{{P}_{2}}={{h}_{1}}{{\rho }_{y}}g-{{\rho }_{Y}}({{h}_{1}}+{{h}_{2}})g+{{\rho }_{X}}{{h}_{2}}g\]
\[\Delta P={{h}_{1}}{{\rho }_{y}}g-{{h}_{1}}{{\rho }_{y}}g-{{h}_{2}}{{\rho }_{Y}}g+{{h}_{1}}{{\rho }_{y}}g\]
\[\Delta P={{h}_{2}}({{\rho }_{X}}-{{\rho }_{y}})g….(5)\]
It is concluded from equation (5) that,
- The value of h2 can be measured in metres i.e., h2 is nothing but the difference in the levels of the liquid X in the two arms
- The difference in the pressures (ΔP) is independent of the value of h1 and the dimensions of the U-tube.
Mercury is used as a monomeric liquid (liquid X) in case of large pressure differences. Alcohol and carbon tetrachloride are used in case of small pressure differences.
Applications of Simple Manometer
- Manometers are attached to the flow meters such as orifice and Venturi meters to measure the flow of fluids.
- Pitot tube uses a manometer to measure the velocity head.
- Consumption of gases in the chemical reactions can be measured using a simple manometer.
Differential Manometer
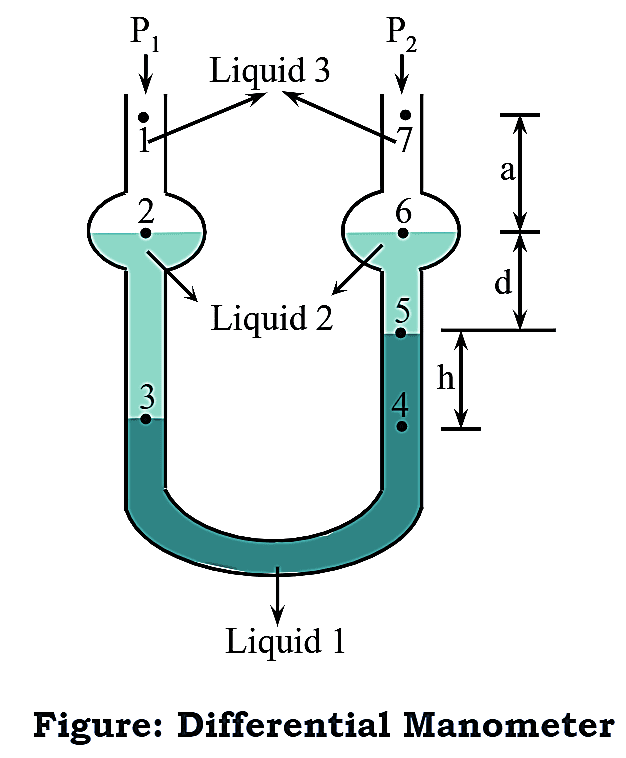
Differential manometer is used for the measurement of small pressure differences and also termed as two-fluid-U-tube manometer. It comprises two immiscible liquids i.e., liquid 1 and 2 of nearly equal densities. Enlarged chambers are constructed in such a way that the meniscus of liquid in the enlarged chambers does not appreciably change or remain unchanged with changes in the reading (h). By employing the same principle of simple manometer, the pressure difference (ΔP) is given by,
\[{{P}_{1}}-{{P}_{2}}=\Delta P=h({{\rho }_{3}}-{{\rho }_{1}})\]
The above equation indicates that for a given ΔP, the smaller the difference between the densities of liquid, the larger will be the reading on manometer.
Applications of Differential Manometer
- These are useful for measuring minute differences in the pressure of the gases.
- Due to the capillarity, they are free from errors and do not require calibration. Instead the micrometer scale is checked.
Inclined Manometer
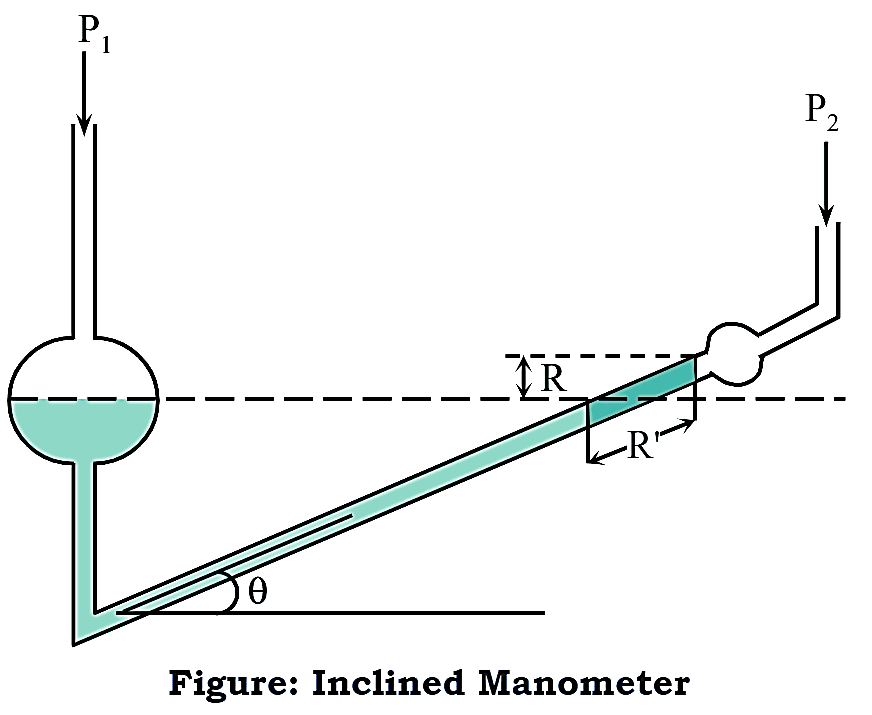
Inclined manometer is used for measuring small pressure differences. It is essentially a modification of simple manometer, wherein one arm of the simple manometer is kept vertical while the other is inclined at an angle θ. The vertical arm has a large enlargement so that when the angle of inclination is changed, the meniscus in the enlargement does not allow any appreciable or measurable movement.
The angle of inclination is such that the fluid meniscus in the inclined arm should move a measurable distance for a small magnitude of R. The distance moved by the meniscus is given by R/sinθ. On making the angle of inclination further small. the fluid in the inclined arm moves through a longer distance (R’). This distance is multiplied by the magnitude of R. the value of which is equivalent to pressure difference.
Therefore,
\[{{P}_{1}}-{{P}_{2}}=g\text{ }R'({{\rho }_{A}}-{{\rho }_{B}})\sin \theta \]
The usage of inclined manometers is limited.