Mesh Analysis in Network theory

After reading this Mesh Analysis topic of electric or network circuits, you will understand the theory and also able to apply it in numerical problems.

---

A mesh is a loop which does not contain any inner loop. Mesh analysis is only applicable to a planar network. A planar network is the one that can be drawn in a plane with no branches crossing one another.

Procedure (steps) for applying mesh analysis:

1. Identify the total number of meshes.
2. Assign the mesh currents.
3. Develop the KVL equation for each mesh.
4. Solve the equations to find the mesh currents.

Note:

• The total number of equations (e) required to solve the network with the help of mesh analysis is

e = b – (N – 1).

where, b is the total number of branches and N is the total number of nodes.

• The direction of mesh currents can be taken in any direction either clockwise or counter-clockwise. But clockwise direction results in a simpler analysis.

Examples

Example1. For the given network, find currents I₁ and I₂ using Mesh analysis.

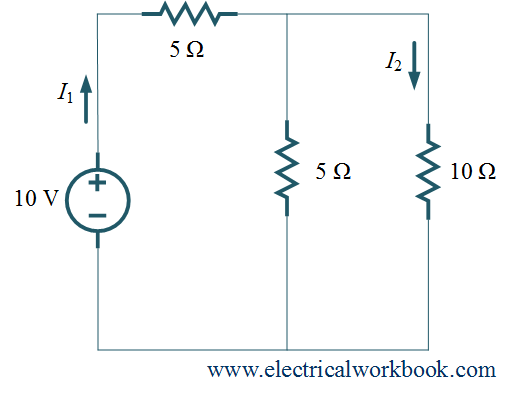
Solution:

Let’s follow the Procedure for applying Mesh Analysis

Step 1: – The total number of meshes is 2.

Step 2: – The mesh currents I₁ and I₂ for mesh 1 and mesh 2 respectively as shown in Figure 1.

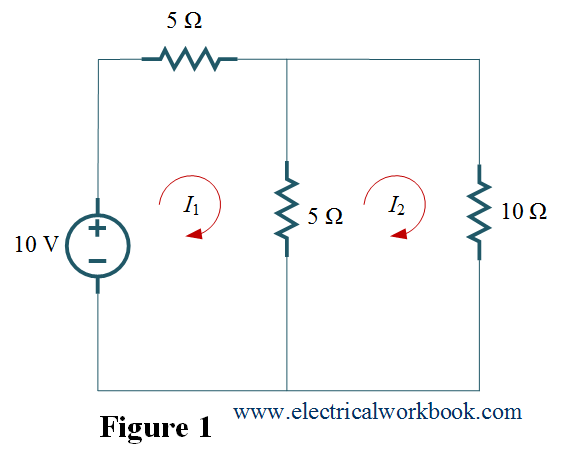
Step 3 and Step 4: – Apply KVL to mesh 1 as shown in Figure 2,

$ – 10 + 5{I_1} + 5({I_1} – {I_2}) = 0$

$2{I_1} – {I_2} = 2$                 ….(1)

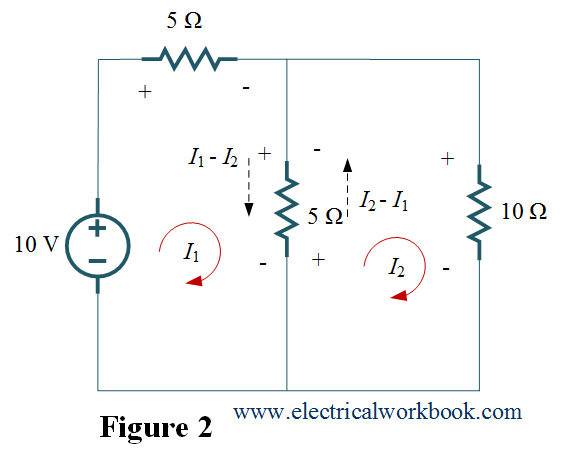
Apply KVL to mesh 2 as shown in Figure 2,

$10{I_2} + 5({I_2} – {I_1}) = 0$

$15{I_2} – 5{I_1} = 0$

${I_1} = 3{I_2}$     ….(2)

Put Eq.(2) in Eq.(1), we get

$5{I_2} = 2$

\[{I_2} = \frac{2}{5}\]

from Eq.(2)

\[{I_1} =  3\left( {\frac{2}{5}} \right){\text{ = }}\frac{{ 6}}{5}{\text{ A}}\]

Thus,

\[{I_2} = \frac{2}{5}{\text{ A}};{I_1} = \frac{{ 6}}{5}{\text{ A}}{\text{.}}\]

Example 2. For the given network, write Mesh equations.

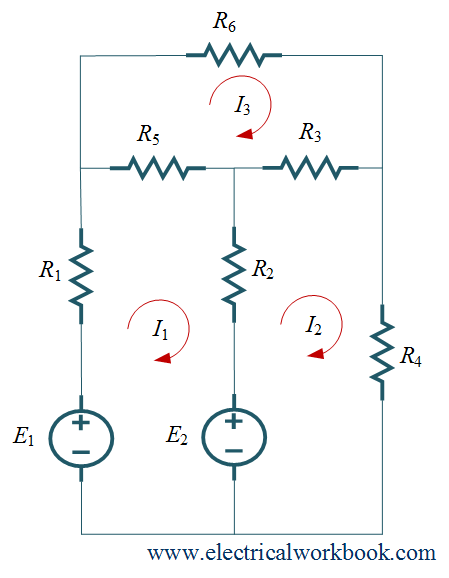
Solution:

Let’s follow the Procedure for applying Mesh Analysis

Step 1: – The total number of meshes is 3.

Step 2: – The mesh currents I₁, I₂ and I₃ for meshes 1, 2 and 3 are shown in Figure given in example 2.

Step 3: – Apply KVL to mesh 1,

 $- {E_1} + {R_1}{I_1} + {R_2}({I_1} – {I_3}) + {R_3}({I_1} – {I_2}) = 0{\text{}}$

Apply KVL to mesh 2,

\[ – {E_2} + {R_3}({I_2} – {I_1}) + {R_4}({I_2} – {I_3}) + {R_4}{I_2} = 0{\text{ }}\]

Apply KVL to mesh 3,

\[{R_6}{I_3} + {R_4}({I_3} – {I_2}) + {R_2}({I_3} – {I_1}) = 0{\text{}}\]