After reading this Norton’s theorem topic of electric or network circuits, you will understand the theory, and also able to apply it in ac and dc circuits numerical problems.
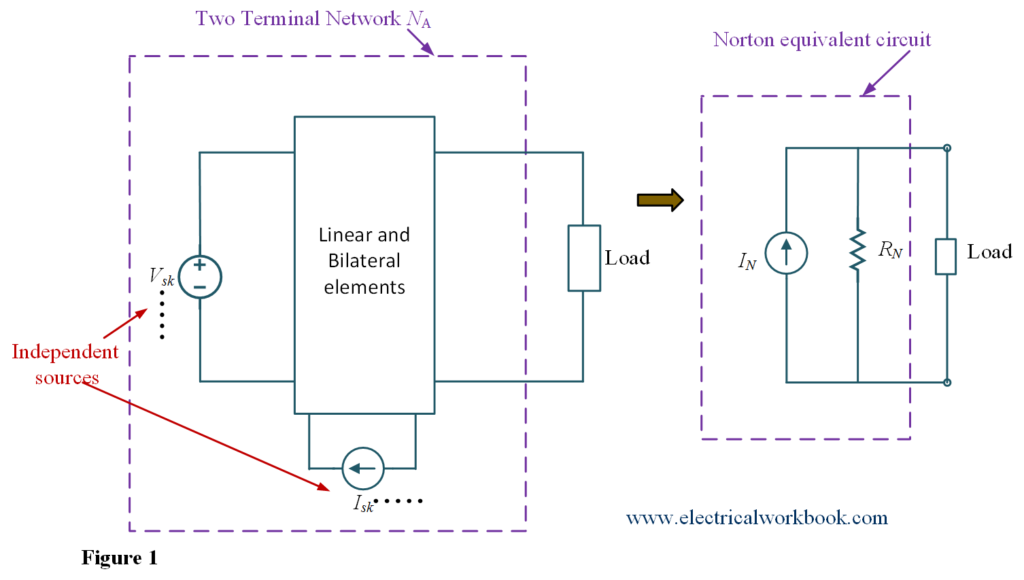
Norton’s theorem states that for two terminal network NA containing linear & bidirectional elements and independent sources is equivalent to a simple network containing an independent current source IN (called as Norton current) in parallel with the resistance RN (called as Norton resistance). The Norton equivalent circuit for network NA shown below in Figure 1.
Procedure (steps) for applying Norton’s theorem: –
- Calculation of Norton current IN
- Calculation of Norton resistance RN for dc circuit and Norton impedance ZN for ac circuit. The Thevenin resistance equal to Norton resistance and the Thevenin impedance equal to Norton impedance. While calculating Norton resistance or impedance, all independent sources are set to zero (voltage source replaced by short circuits and current source replaced by open circuits).
- Develop the Norton equivalent circuit and find the unknown parameter.
Norton theorem Example based on the DC circuit
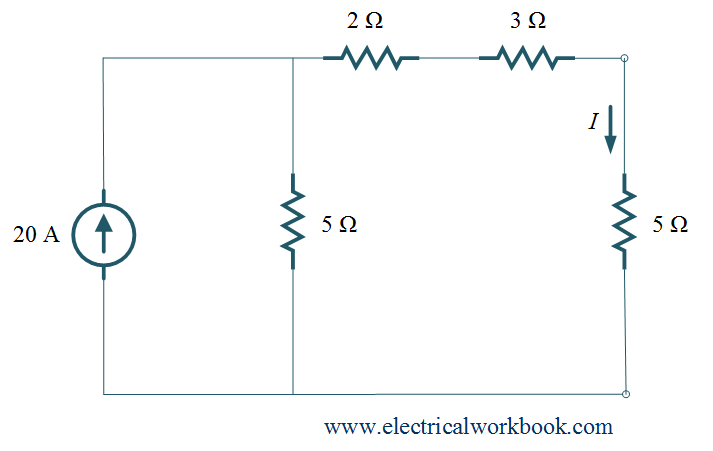
Q For the given network, find the current I passes through 5 $\Omega $ using Norton equivalent circuit.
Step 1: – Norton current IN calculation
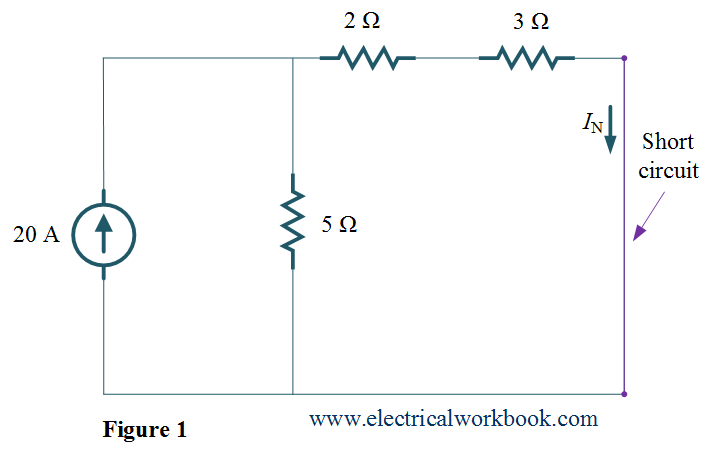
Remove 5 $\Omega $ branch from the circuit and replace it with a short circuit as shown in Figure 1 and let us assign the current IN (also called as Norton current) passes through the short circuit. By applying the current divider rule in Figure 1 gives
\[{I_{\text{N}}} = \frac{{20}}{{5 + 2 + 3}}\left( 5 \right) = 10{\text{ A}}{\text{.}}\]
Step 2: – Norton Resistance RN calculation
Replace 20 A current source as open circuit as shown in Figure 2, Thus RN for the circuit is
\[{R_{\text{N}}} = 3 + 2 + 5 = 10{\text{ }}\Omega \]

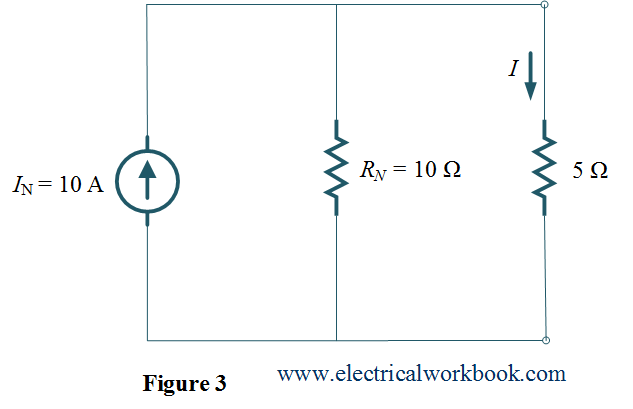
Step 3: – The Norton equivalent circuit as shown in Figure 3, and the current through 5 $\Omega $ branch calculated using current divider rule gives
\[I = \frac{{10}}{{5 + 10}}\left( 10 \right) = 6.67{\text{ A}}{\text{.}}\]
Norton theorem Example based on AC circuit
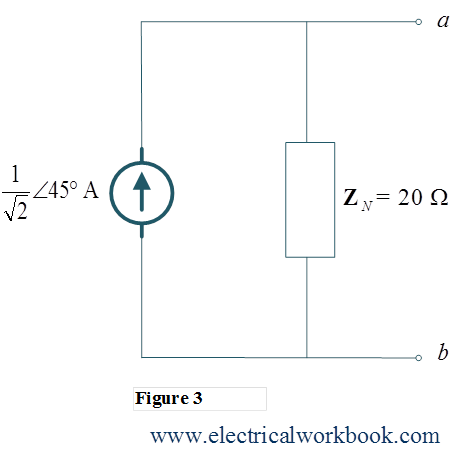
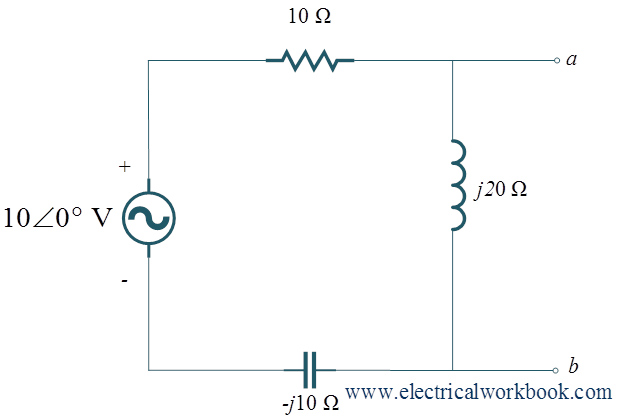
Q For the given network, find the Norton equivalent circuit between the terminals a and b.
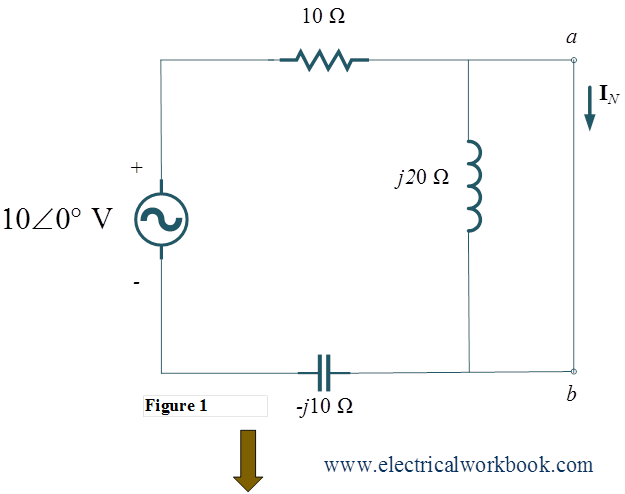
Step 1: – Norton current ${{\mathbf{I}}_{{\text{N}}}}$ calculation
By applying Ohm’s law to find ${{\mathbf{I}}_{{\text{N}}}}$ as shown in Figure 1, we get,
\[{{\mathbf{I}}_{{\text{N}}}} = \frac{{10\angle 0^\circ }}{{10 – j10}} = \frac{1}{{1 – j1}}{\text{ = }}\frac{1}{{\sqrt 2 }}\angle 45^\circ {\text{ A}}\]
Step 2: – Norton Impedance ${{\mathbf{Z}}_{{\text{N}}}}$ calculation
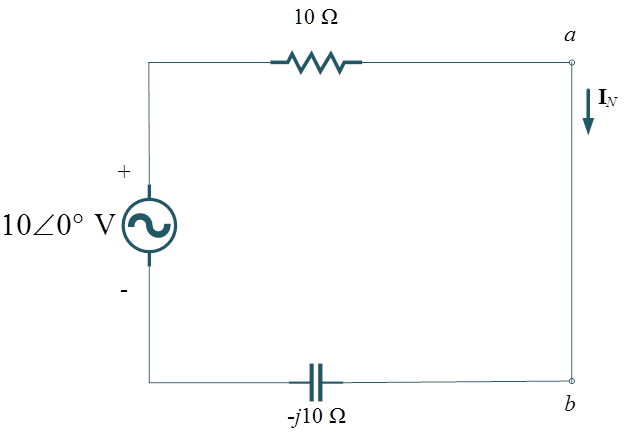
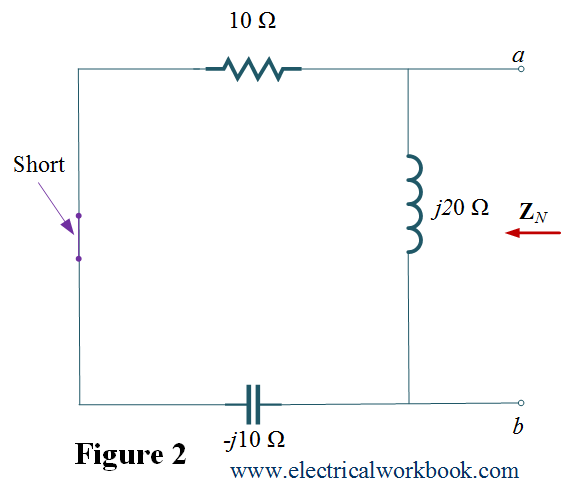
Replace ${\text{1}}0\angle 0^\circ$ V voltage source as short circuit as shown in Figure 2 gives
\[{{\mathbf{Z}}_{\text{N}}} = ((10 – j10)||j20) = \frac{{(10 – j10) \times j20}}{{(10 – j10) + j20}} = 20{\text{ }}\Omega \]
\[{\text{Thus, }}{{\mathbf{I}}_{{\text{N}}}}{\text{ = }}\frac{1}{{\sqrt 2 }}\angle 45^\circ {\text{ A}},{\text{ }}{{\mathbf{Z}}_{\text{N}}} = 20{\text{ }}\Omega \]
Step 3: – The Norton equivalent circuit as shown in Figure 3