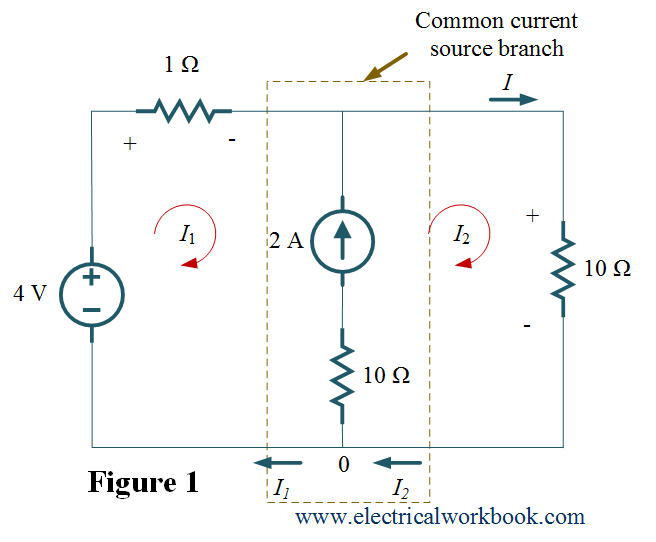
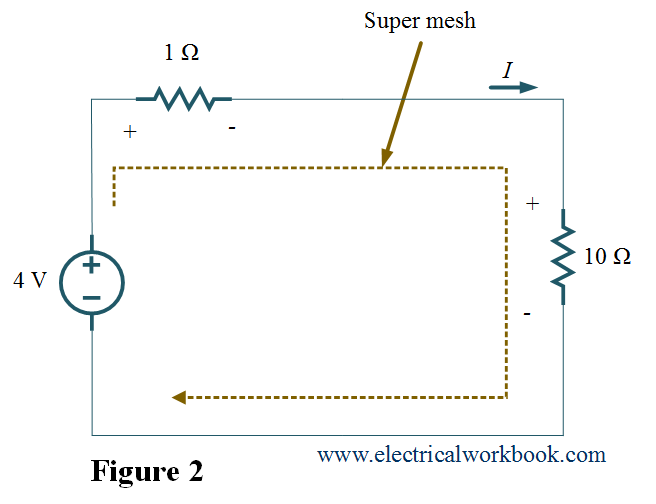
A supermesh forms when two meshes have a common current source (dependent or independent). Consider a circuit as shown below in Figure 1 in which the current source branch is common between meshes 1 and 2 so remove the current source branch and supermesh forms as shown in Figure 2.
Procedure (steps) for applying mesh analysis:
- Identify the total number of meshes.
- Assign the mesh currents and check for supermesh in the circuit.
- If supermesh found, develop the KVL equation for it.
- Solve the equations to find the mesh currents.
Example
Example 1. For the given network, find current I using Mesh analysis.
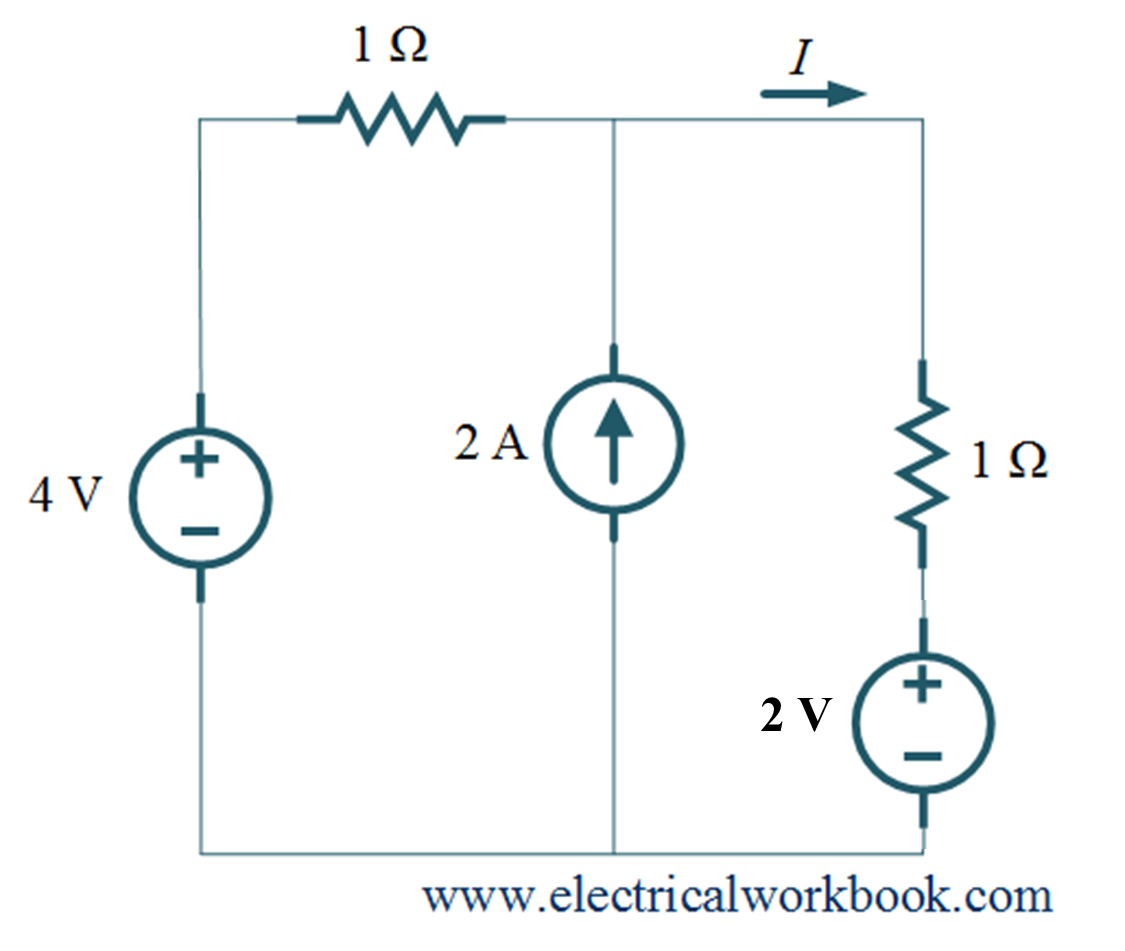
As shown above, Figure is given in example 1, 2 A current source is connected between meshes 1 and 2 so this problem is based on supermesh.
Step 1: – The total number of meshes is 2.
Step 2: – Let us assign mesh currents I1 and I2 for meshes 1 and 2 respectively as shown in Figure 1. As shown in Figure 1, 2 A current source should be removed from the circuit because 2 A current source is connected between meshes 1 and 2.
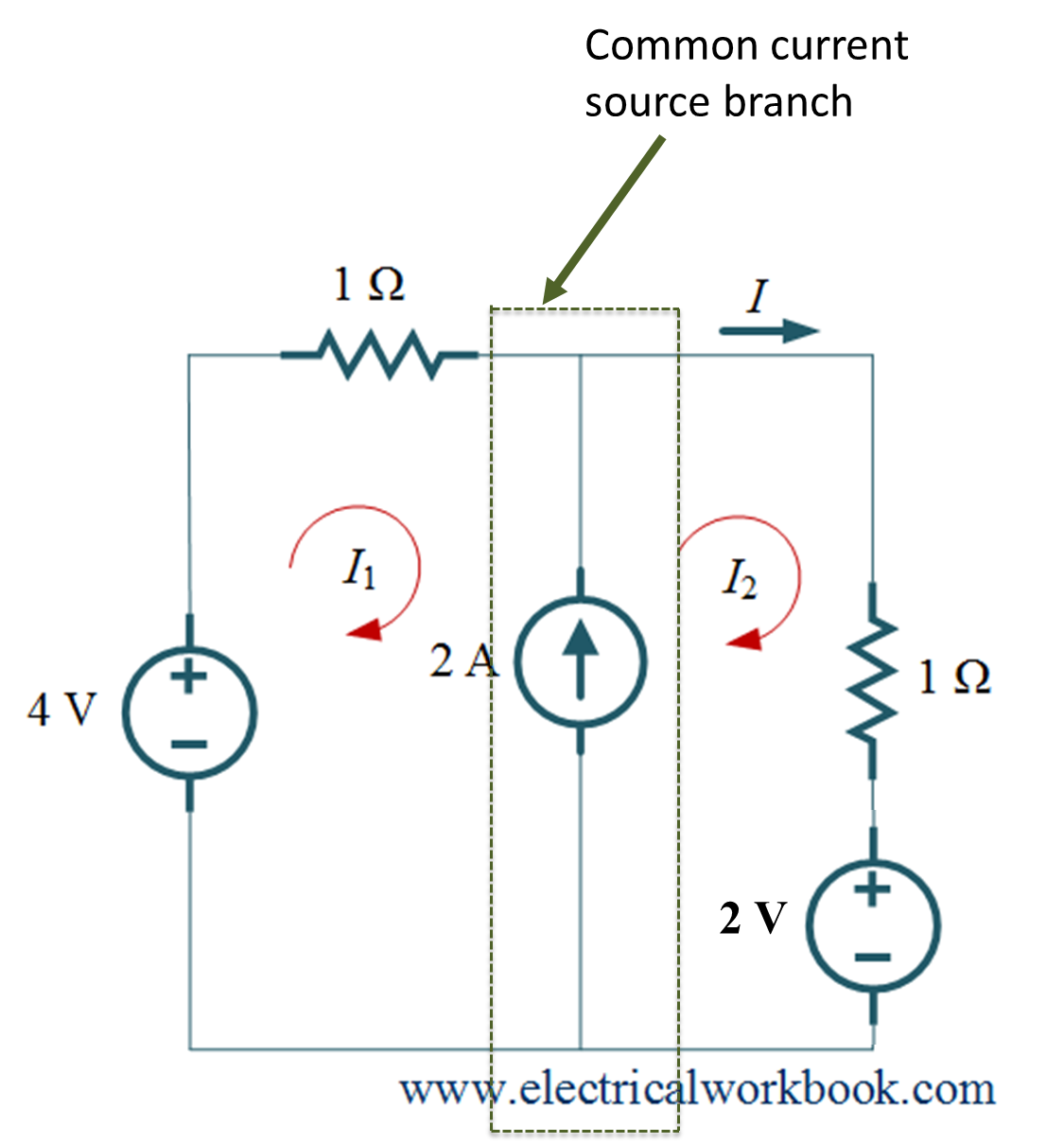
Figure 1.
Step 3: – The reduced circuit having supermesh shown in Figure 2.
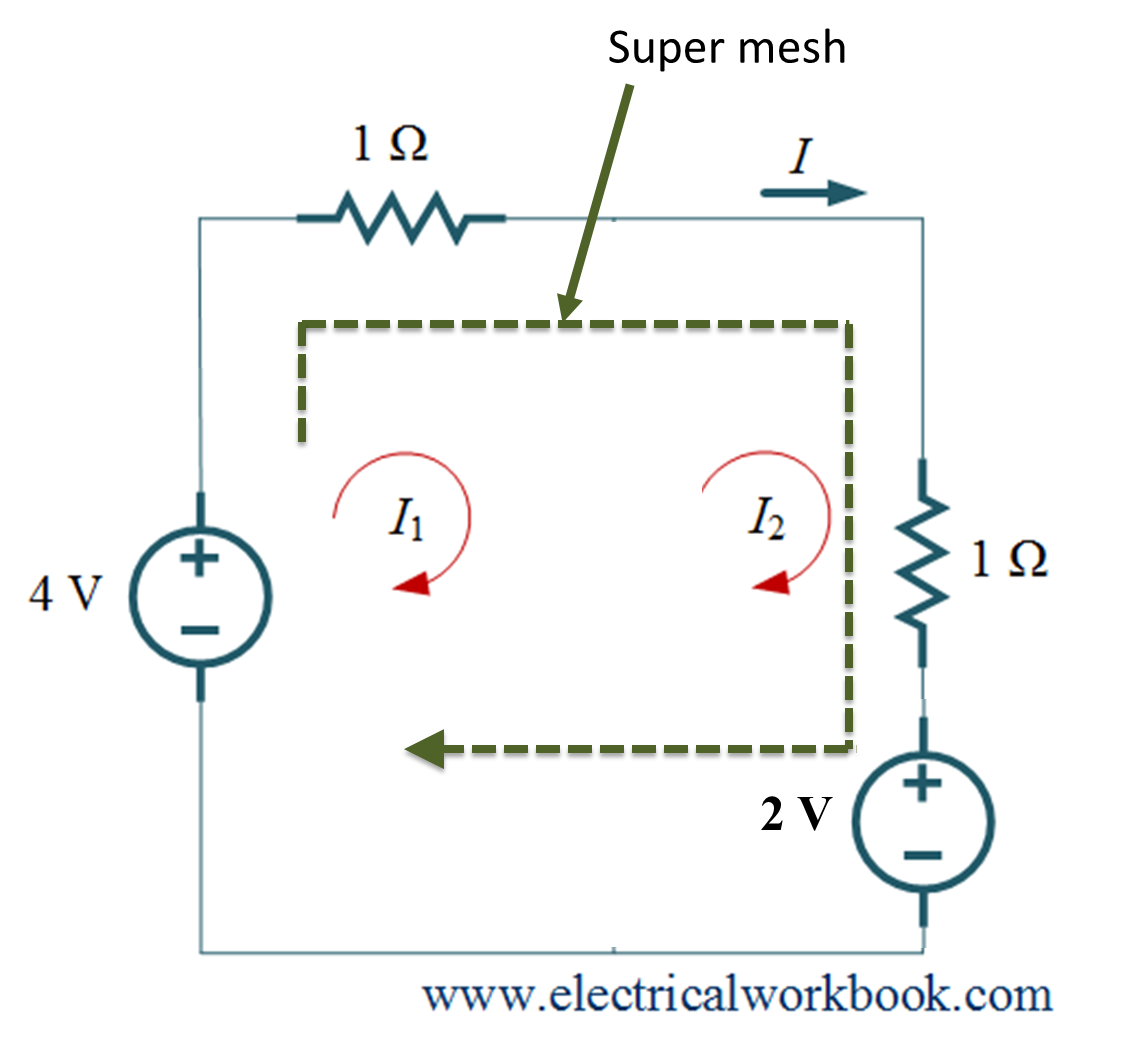
Figure 2.
Apply KVL to supermesh
\[{\text{ – 4 + }}{I_1} + {I_2} + 2 = 0\]
${I_1} + {I_2} = 2$ ….(1)
Apply KCL to node 0,
\[{I_2} – {I_1} = 2{\text{ }}\]
${I_2} = {I_1} + 2$ ….(2)
Put equation (2) in equation (1), we get
\[{I_1} + {I_1} + 2 = 2\]
\[2{I_1} + 2 = 2\]
${I_1} = 0{\text{ A }}$ ….(3)
From Equation (1) ,
\[{I_1} + {I_2} = 2\]
Put equation (3) in equation (1), we get
\[0 + {I_2} = 2\]
\[{I_2} = 2\]
also \[I = {I_2}\]
Therefore,
\[I = 2{\text{ A}}{\text{.}}\]