In this topic, you study Transformer Ratio (Voltage Ratio, Current Ratio & Turns Ratio).
Fig. 1 shows a transformer with its secondary winding connected to the load.
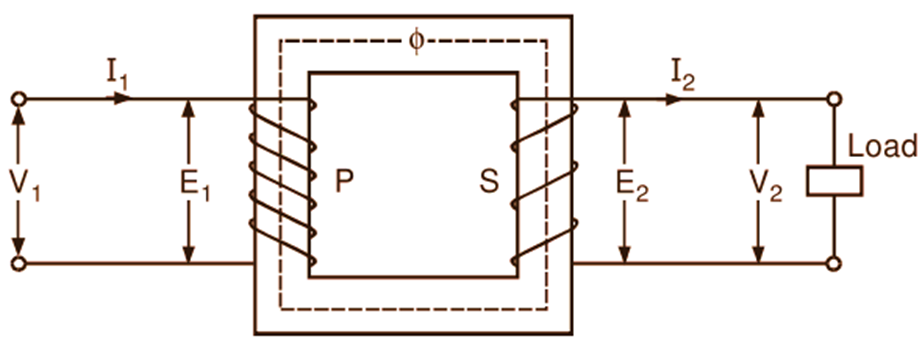
Fig. 1: Voltage and current ratios
Voltage Ratio: Let ${{\text{N}}_{1}}$ and ${{\text{N}}_{2}}$ be the number of turns of the primary and secondary windings respectively, ${{\text{E}}_{1}}$ and ${{\text{E}}_{1}}$ the r.m.s. values of induced emf in the corresponding windings. Then
\[{{\text{E}}_{1}}=4.44\text{ }{{\phi }_{\text{m}}}\text{f }{{\text{N}}_{1}}\text{ volts}\]
and
\[{{\text{E}}_{2}}=4.44\text{ }{{\phi }_{\text{m}}}\text{f }{{\text{N}}_{2}}\text{ volts}\]
Thus,
\[\frac{{{\text{E}}_{1}}}{{{\text{E}}_{2}}}\text{ = }\frac{{{\text{N}}_{1}}}{{{\text{N}}_{2}}}….(1)\]
Now, if the voltage applied across the primary winding is ${{\text{V}}_{1}}$ and terminal voltage of the secondary winding is ${{\text{V}}_{2}}$ as illustrated in Fig. 1, then at no load (i.e. when the secondary is on open circuit),
\[{{\text{V}}_{2}}=\text{ }{{\text{E}}_{2}}\]
Also, the primary current being very small under this condition, ${{\text{V}}_{1}}$ is numerically almost equal to ${{\text{E}}_{1}}$. Hence, the Equation (1) gives,
\[\frac{{{\text{E}}_{1}}}{{{\text{E}}_{2}}}\text{ = }\frac{{{\text{V}}_{1}}}{{{\text{V}}_{2}}}\text{ =}\frac{{{\text{N}}_{1}}}{{{\text{N}}_{2}}}….(2)\]
Voltage Ratio
The primary and the secondary terminal voltages of a transformer are proportional to the respective number of turns. The ratio of the primary to secondary terminal voltage is known as voltage ratio.
Turns Ratio
The ratio of the primary to secondary turns is known as turns ratio of the transformer. At no load, voltage and turns ratios are equal. The impedances of the transformer windings being small, even at full load, they are nearly equal.
Transformation Ratio
More often, the ratio of the secondary voltage to the primary voltage is termed as transformation ratio and denoted by the letter K. Therefore, from the Equation (1),
Transformation ratio,
\[\text{K}=\frac{{{\text{E}}_{2}}}{{{\text{E}}_{1}}}\text{ = }\frac{{{\text{V}}_{2}}}{{{\text{V}}_{1}}}\text{ =}\frac{{{\text{N}}_{2}}}{{{\text{N}}_{1}}}….(3)\]
Step up transformer
If $\text{K}>1$ i.e. ${{\text{V}}_{2}}>{{\text{V}}_{1}}$, transformer is called a step up transformer. It is that transformer which receives electrical energy at one voltage and delivers it at a higher voltage.
Step down transformer
If $\text{K}<1$ i.e. ${{\text{V}}_{2}}<{{\text{V}}_{1}}$, transformer is called a step-down transformer. It is the transformer which receives electrical energy at one voltage and delivers it at a lower voltage.
One to one transformer
If $\text{K}=1$ i.e. ${{\text{V}}_{2}}={{\text{V}}_{1}}$, transformer is called a one to one transformer. Obviously, such a transformer transfers electrical energy from one circuit to another circuit without any change in the voltage.
Current Ratio
Further, since the transformer transfers electrical power from one circuit to another circuit very efficiently with negligible power loss,
Power input = Power output
$\text{since, P = VI}\cos \phi \text{ }$
Thus,
\[{{\text{V}}_{1}}{{\text{I}}_{1}}\cos {{\phi }_{1}}={{\text{V}}_{2}}{{\text{I}}_{2}}\cos {{\phi }_{2}}\]
where ${{\text{I}}_{1}}$ and ${{\text{I}}_{2}}$ are the currents in the primary and the secondary circuit respectively, and $\cos {{\phi }_{1}}$ and $\cos {{\phi }_{2}}$ are the corresponding power factors. But for a transformer, the primary and the secondary power factors are also nearly equal, particularly at full load.
\[{{\text{V}}_{1}}{{\text{I}}_{1}}={{\text{V}}_{2}}{{\text{I}}_{2}}\]
Or,
\[\frac{{{\text{I}}_{1}}}{{{\text{I}}_{2}}}\text{=}\frac{{{\text{V}}_{2}}}{{{\text{V}}_{1}}}….(4)\]
Combining the results obtained in the Equations (3) and (4), we have
\[\frac{{{\text{V}}_{2}}}{{{\text{V}}_{1}}}\text{ }=\frac{{{\text{I}}_{1}}}{{{\text{I}}_{2}}}\text{=}\frac{{{\text{N}}_{2}}}{{{\text{N}}_{1}}}=\text{K}\]
Thus, from the above expression, it is clear that the primary and the secondary currents of a transformer are inversely proportional to the respective turns or voltages.