What is Wein Bridge? Theory, Diagram & Derivation

In the Wein bridge, an inductance is measured by comparison with a standard variable capacitance.

Let

L₁ = unknown inductance of resistance R₁

R₂, R₃, R₄ = known non-inductive resistors

C₄ = Variable standard capacitance

The fourth arm CD contains a resistor R₄ and a capacitor C₄ in parallel. The total impedance of the two will give the impedance of the arm. (Fig. 1).

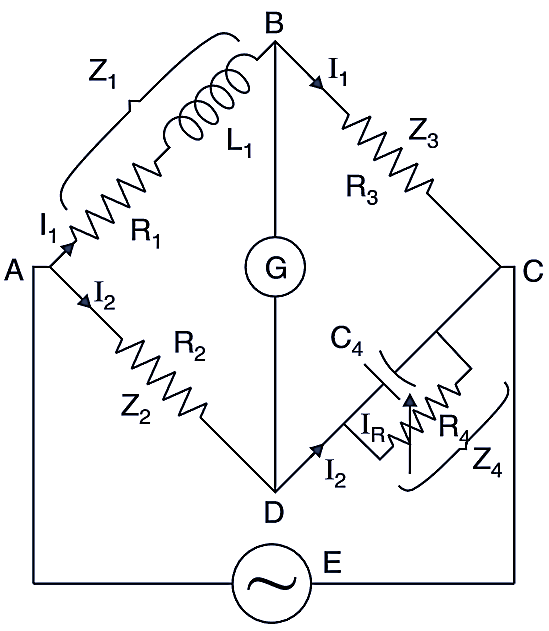
Fig. 1: Wein Bridge

As

\[\frac{1}{{{\text{Z}}_{\text{4}}}}\text{ = }\frac{1}{{{\text{X}}_{\text{C4}}}}\text{ +}\frac{1}{{{\text{R}}_{\text{4}}}}\text{ }\]

Now, we will find value of Z₄

\[{{\text{Z}}_{\text{4}}}\text{ = }\frac{{{\text{X}}_{\text{C4}}}\cdot {{\text{R}}_{\text{4}}}}{{{\text{X}}_{\text{C4}}}+{{\text{R}}_{\text{4}}}}\]

Since,

\[{{\text{X}}_{\text{C4}}}\text{ = }\frac{\text{1}}{2\text{  }\!\!\pi\!\!\text{  f }{{\text{C}}_{\text{4}}}}\text{= }\frac{\text{1}}{\omega {{\text{C}}_{\text{4}}}}\]

Thus,

\[{{\text{Z}}_{\text{4}}}\text{ = }\frac{{{\text{R}}_{\text{4}}}/\omega {{\text{C}}_{\text{4}}}}{\text{1}+{{\text{R}}_{\text{4}}}\cdot \omega {{\text{C}}_{\text{4}}}\cdot \omega {{\text{C}}_{\text{4}}}}\]

or

\[{{\text{Z}}_{\text{4}}}\text{ = }\frac{{{\text{R}}_{\text{4}}}}{\omega {{\text{C}}_{\text{4}}}}\cdot \frac{\omega {{\text{C}}_{\text{4}}}}{\text{1}+{{\text{R}}_{\text{4}}}\cdot \omega {{\text{C}}_{\text{4}}}\cdot \omega {{\text{C}}_{\text{4}}}}\]

\[\text{= }\frac{{{\text{R}}_{\text{4}}}}{\text{1}+{{\text{R}}_{\text{4}}}\cdot \omega {{\text{C}}_{\text{4}}}}\]

In j notation,

\[{{\text{Z}}_{\text{4}}}\text{ = }\frac{{{\text{R}}_{\text{4}}}}{\text{1}+\text{j}\omega {{\text{C}}_{\text{4}}}\cdot {{\text{R}}_{\text{4}}}}\]

At balance condition:

\[{{\text{Z}}_{\text{1}}}{{\text{Z}}_{\text{4}}}\text{ = }{{\text{Z}}_{\text{2}}}{{\text{Z}}_{\text{3}}}\]

Using j notation:

\[\left( {{\text{R}}_{\text{1}}}\text{+ j}\omega {{\text{L}}_{\text{1}}} \right)\frac{{{\text{R}}_{\text{4}}}}{\text{1}+\text{j}\omega {{\text{C}}_{\text{4}}}\cdot {{\text{R}}_{\text{4}}}}\text{ = }{{\text{R}}_{\text{2}}}{{\text{R}}_{\text{3}}}\]

\[{{\text{R}}_{\text{1}}}{{\text{R}}_{\text{4}}}\text{+ j}\omega {{\text{L}}_{\text{1}}}{{\text{R}}_{\text{4}}}\text{ = }{{\text{R}}_{\text{2}}}{{\text{R}}_{\text{3}}}\text{+j}\omega {{\text{C}}_{\text{4}}}\cdot {{\text{R}}_{\text{2}}}{{\text{R}}_{\text{3}}}{{\text{R}}_{\text{4}}}\]

Now equating real terms

\[{{\text{R}}_{\text{1}}}{{\text{R}}_{4}}={{\text{R}}_{\text{2}}}{{\text{R}}_{\text{3}}}\]

or

\[{{\text{R}}_{\text{1}}}=\frac{{{\text{R}}_{\text{2}}}{{\text{R}}_{\text{3}}}}{{{\text{R}}_{4}}}\]

Equating imaginary terms

\[\text{j}\omega {{\text{L}}_{\text{1}}}{{\text{R}}_{\text{4}}}=\text{ j}\omega {{\text{C}}_{\text{4}}}\cdot {{\text{R}}_{\text{2}}}{{\text{R}}_{\text{3}}}{{\text{R}}_{\text{4}}}\]

or

\[{{\text{L}}_{\text{1}}}={{\text{R}}_{\text{2}}}{{\text{R}}_{\text{3}}}{{\text{C}}_{\text{4}}}\]

The inductance L₁ can be found out, as all other quantities are known.

Advantages of Wein bridge

The advantages of Wein bridge are:

1. The equations are independent of frequency.
2. The bridge is very useful for the measurement of a wide range of inductance at audio frequency (20 Hz to 20 kHz).

Disadvantage of Wein bridge

1. This requires a variable standard capacitor which is very expensive for getting a good accuracy.