In this topic, you study Voltage Divider Rule – Derivation, Formula & Theory.
Consider the network of Fig. 1 composed of three series-connected resistors and a voltage source of V volts.
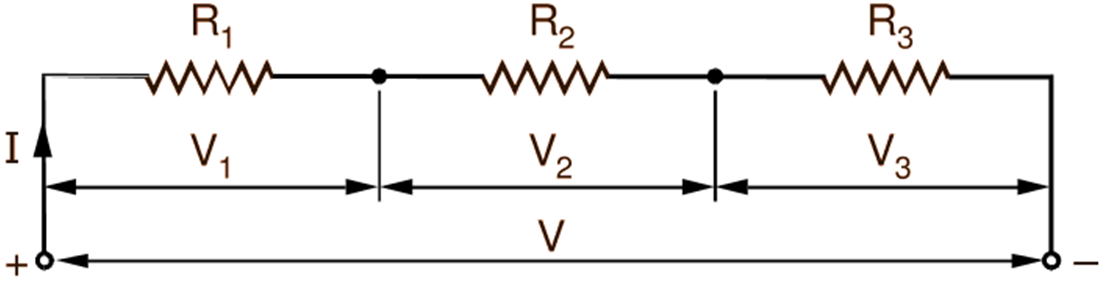
Fig. 1: Voltage Divider Rule
Here, it is obvious that total resistance of the network,
\[\text{R}={{\text{R}}_{1}}+\text{ }{{\text{R}}_{2}}+\text{ }{{\text{R}}_{3}}\]
Circuit current,
\[\text{I}=\frac{\text{V}}{\text{R}}\]
Hence,
\[{{\text{V}}_{1}}=\text{I}{{\text{R}}_{1}}=\frac{\text{V}}{\text{R}}\times {{\text{R}}_{1}}\]
\[=\frac{\text{V}}{\text{(}{{\text{R}}_{1}}+\text{ }{{\text{R}}_{2}}+\text{ }{{\text{R}}_{3}})}\times {{\text{R}}_{1}}\]
\[{{\text{V}}_{1}}=\frac{{{\text{R}}_{1}}}{\text{(}{{\text{R}}_{1}}+\text{ }{{\text{R}}_{2}}+\text{ }{{\text{R}}_{3}})}\times \text{V}\]
Also,
\[{{\text{V}}_{2}}=\text{I}{{\text{R}}_{2}}=\frac{\text{V}}{\text{R}}\times {{\text{R}}_{2}}\]
\[=\frac{\text{V}}{\text{(}{{\text{R}}_{1}}+\text{ }{{\text{R}}_{2}}+\text{ }{{\text{R}}_{3}})}\times {{\text{R}}_{2}}\]
\[{{\text{V}}_{2}}=\frac{{{\text{R}}_{2}}}{\text{(}{{\text{R}}_{1}}+\text{ }{{\text{R}}_{2}}+\text{ }{{\text{R}}_{3}})}\times \text{V}\]
Also,
\[{{\text{V}}_{3}}=\text{I}{{\text{R}}_{1}}=\frac{\text{V}}{\text{R}}\times {{\text{R}}_{3}}\]
\[=\frac{\text{V}}{\text{(}{{\text{R}}_{1}}+\text{ }{{\text{R}}_{2}}+\text{ }{{\text{R}}_{3}})}\times {{\text{R}}_{3}}\]
\[{{\text{V}}_{3}}=\frac{{{\text{R}}_{3}}}{\text{(}{{\text{R}}_{1}}+\text{ }{{\text{R}}_{2}}+\text{ }{{\text{R}}_{3}})}\times \text{V}\]
Therefore, in general, if there are n such series-connected resistors in the network, then we have
\[{{\text{V}}_{\text{k}}}=\frac{{{\text{R}}_{\text{k}}}}{\text{(}{{\text{R}}_{1}}+\text{ }{{\text{R}}_{2}}+..+\text{ }{{\text{R}}_{\text{k}}}+..+{{\text{R}}_{\text{n}}})}\times \text{V}\]
….(1)
where Vk is the voltage drop across the resistor Rk and V is the impressed voltage across all the series-connected resistors.
Equation (1) is frequently referred to as the voltage-divider rule. In words, it can be stated as follows .
In a circuit composed of n series-connected resistors and a voltage source of V volts, voltage drop Vk appearing across the terrninals of resistor Rk is given by
\[{{\text{V}}_{\text{k}}}=\frac{{{\text{R}}_{\text{k}}}}{\text{(}{{\text{R}}_{1}}+\text{ }{{\text{R}}_{2}}+..+\text{ }{{\text{R}}_{\text{k}}}+..+{{\text{R}}_{\text{n}}})}\times \text{V}\]
This rule is very useful in finding the voltage across a single resistor in a series circuit without finding the circuit current.