A DC series motor is a type of direct current (DC) motor where the field winding is connected in series with the armature winding. As a result, the same current flows through both the armature and the field winding. This design gives the motor unique characteristics, including high starting torque and speed that varies with the load.
Connection diagram of DC Series Motor
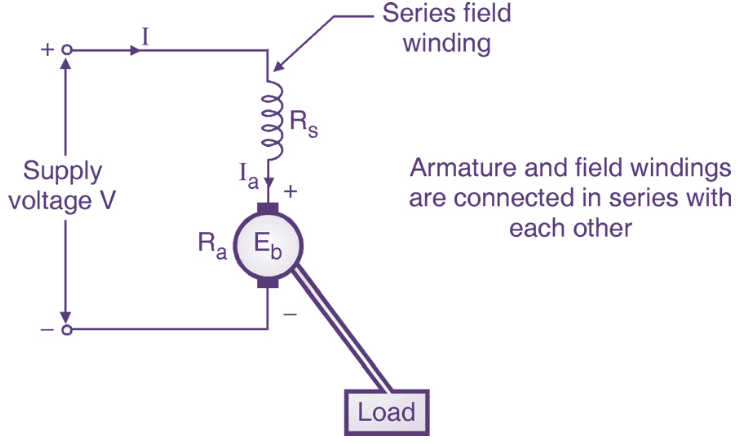
Fig. 1: DC Series Motor.
In the DC series motor, the armature and field windings are connected in series with each other as shown in Fig. 1. The resistance of the series field winding (Rs) is much smaller as compared to that of the armature resistance (Ra).
Construction of DC Series Motor
A DC series motor is a type of DC motor where the field windings are connected in series with the armature winding. Its main components include:
- Armature Winding: A rotating part where current flows and interacts with the magnetic field to produce torque.
- Series Field Winding: A coil made of thick wire with fewer turns to carry the same current as the armature.
- Commutator: A device that reverses the current direction in the armature to maintain unidirectional torque.
- Brushes: Carbon blocks that provide electrical contact to the rotating commutator.
- Yoke and Poles: Provide structural support and house the magnetic field.
Voltage and Current relations in DC Series Motor
The total current I supplied by the supply voltage (see Figure 1) is same as the field current Is and armature current Ia.
\[I={{I}_{s}}={{I}_{a}}\]
The total supply voltage V is given by,
V = Volatge across feild + Volatge across field
\[={{I}_{a}}{{R}_{a}}+({{E}_{b}}+{{I}_{a}}{{R}_{a}}+{{V}_{brush}})\]
But,
\[{{I}_{s}}={{I}_{a}}\]
\[V={{E}_{b}}+{{I}_{a}}{{R}_{a}}+{{I}_{a}}{{R}_{s}}+\text{ Brush drop}\]
Neglecting the brush drop we get,
\[V={{E}_{b}}+{{I}_{a}}({{R}_{a}}+{{R}_{s}})\]
The flux produced is proportional to the field current. But in series motor, the field current is same as armature, the armature current.
\[\phi \propto {{I}_{a}}\]
Since the armature current flows through the series field winding, the flux is proportional to the field current as well.
\[\phi \propto {{I}_{s}}\]
The armature current Ia and hence the field current Is will be dependent on the load. With increase in load Ia and Is will Increase. Hence in a DC series motor the flux ϕ does not remain constant. So the DC series motor is not a constant flux motor.
Characteristics of DC Series Motor
Torque – Armature Current Characteristics of DC series motor

Fig. 2: DC Series Motor Torque – Armature Current Characteristics.
For the DC series motor, the torque produced is given by,
\[{{T}_{a}}\propto \phi {{I}_{a}}\]
But,
\[\phi \propto {{I}_{a}}\]
∴
\[{{T}_{a}}\propto I_{a}^{2}\]
Where, Ta represents the gross torque produced by the motor.
As the torque is proportional to square of armature current, the starting torque of DC series motor is much higher than that of DC shunt motor. The torque armature current characteristics of a DC series motor is as shown in Fig. 2. The characteristics of Ta versus Ia can be divided into two parts :
- In part-I, the torque is proportional to the square of armature current. (upto point S in Fig. 2). Hence torque increases exponentially with increase in armature current.
- But at point S, the saturation of the field electromagnet may take place. It means that there is no change in flux even when there is a change in field current. Hence in part II of the characteristics in Fig. 2, the torque produced is directly proportional to the armature current and not proportion to its square. Hence the torque increases linearly. The dotted characteristics of Fig. 2 shows the variation of shaft torque Tsh with the armature current. Note that,
\[{{T}_{sh}}={{T}_{a}}-{{I}_{f}}\]
Tsh = 0 at no load i.e. when Ia = Ia0 and the curve of Tsh can be obtained by subtracting the constant lost torque from the gross torque Ta.
Speed – Armature Current Characteristics of DC series motor
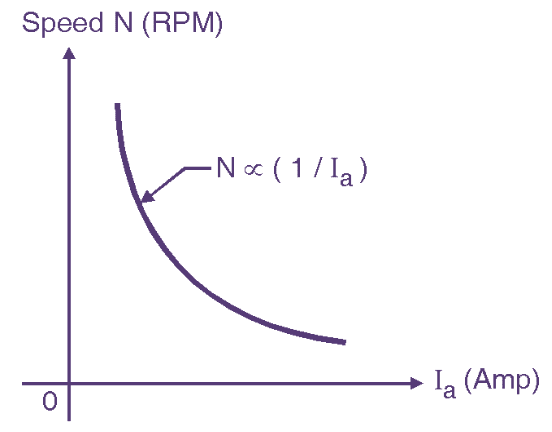
Fig. 3: DC Series Motor Speed – Armature Current Characteristics.
The speed-armature current characteristics of a DC series motor is shown in Fig. 3. We know that,
\[N\propto \frac{{{E}_{b}}}{\phi }\]
Substituting the value of Eb as Eb = V – Ia (Ra + Rs) and ϕ ∝ Ia we get,
\[N\propto \frac{V-{{I}_{a}}\left( {{R}_{a}}+{{R}_{s}} \right)}{K{{I}_{a}}}\]
Due to the small values of Ra and Rs Eb ≈ V which is constant,
\[N\propto \frac{1}{{{T}_{a}}}\]
Hence the speed decreases with increase in Ia. as shown in Fig. 1.
Speed – Torque Characteristic of DC series motor

Fig. 4: DC Series Motor Speed – Torque Characteristics.
The speed-torque characteristics of a DC series motor is as shown in Fig. 4.
We know that,
\[T\propto I_{a}^{2}\text{ and }N\propto \frac{1}{{{I}_{a}}}\]
\[{{I}_{a}}\propto \sqrt{T}\text{ and }N\propto \frac{1}{\sqrt{T}}\]
This shows that the speed decreases increase in the value of torque (i.e. with increase in load). Note that the nature of speed-torque characteristics is same as that of speed-armature current characteristics. DC series motors are preferred for the traction applications because of their capability to generate a high starting torque.
Advantages of DC Series Motor
- Provides high starting torque, suitable for heavy loads.
- Compact and lightweight compared to other motors of similar power ratings.
- Simple construction and low initial cost.
- High efficiency at full load.
Disadvantages of DC Series Motor
- Cannot be used without a load (can overspeed dangerously).
- Speed regulation is poor under varying loads.
- Maintenance is required due to brushes and commutator wear.
- Not suitable for precise speed control.
Why is DC Series Motor Never Started on No Load?
For a DC series motor ϕ ∝ Ia. At no load Ia is small, hence also is small. But motor speed is inversely proportional to ϕ.
\[\text{N}\propto \frac{1}{\phi }\]
Hence at no load when is small and the motor speed can be excessively high. This can damage the motor mechanically. In order to avoid this, we should never start the DC series motor on no load.
Uses of DC Series Motor
Transportation Systems
- Electric Trains and Trams: DC series motors provide the high starting torque required to move heavy train cars.
- Trolleys and Locomotives: Used for propulsion systems in traction applications.
Lifting Equipment
- Cranes and Hoists: Ideal for lifting and lowering heavy loads due to their ability to generate strong torque at low speeds.
- Elevators: Used in industrial and commercial settings for efficient and reliable operation.
Automotive Industry
- Starter Motors for Vehicles: DC series motors are used in car starters because they can generate the high torque needed to crank the engine.
Industrial Applications
- Conveyor Belts: For heavy material handling in industries.
- Rolling Mills and Presses: To handle large mechanical loads in manufacturing processes.
Applications of DC Series Motor
Series motor characteristics indicate that it develops very high starting torque and it has adjustable varying speed. Therefore, for any load which needs high starting torque, series motor is the only suitable DC motor. Series motors are very widely used for the following applications :
- Electric trains,
- Diesel electric locomotives,
- Cranes,
- Hoists,
- Trolley cars and trolley buses,
- Rapid-transit systems,
- Conveyers etc.
Characteristics of DC Series Motor
- High Starting Torque: Torque is directly proportional to the square of the current.
- Variable Speed: Speed decreases with an increase in load due to higher current draw.
- Non-linear Torque-Speed Relationship: Torque increases significantly with current, but speed decreases.
Summary of DC Series Motor
