After reading this topic Peak time $({t_p})$ in Time response of a second-order control system for subjected to a unit step input underdamped case, you will understand the theory, expression, plot, and derivation.
A block diagram of the second order closed-loop control system with unity negative feedback is shown below in Figure 1,

The general expression for the time response of a second order control system or underdamped case is
\[c(t) = 1 – \frac{{{e^{ – \xi {\omega _n}t}}}}{{\sqrt {1 – {\xi ^2}} }}\sin \left[ {({\omega _n}\sqrt {1 – {\xi ^2}} )t + \theta } \right]…(1)\]
Also Equation 1, is plotted in Figure 2 as shown below
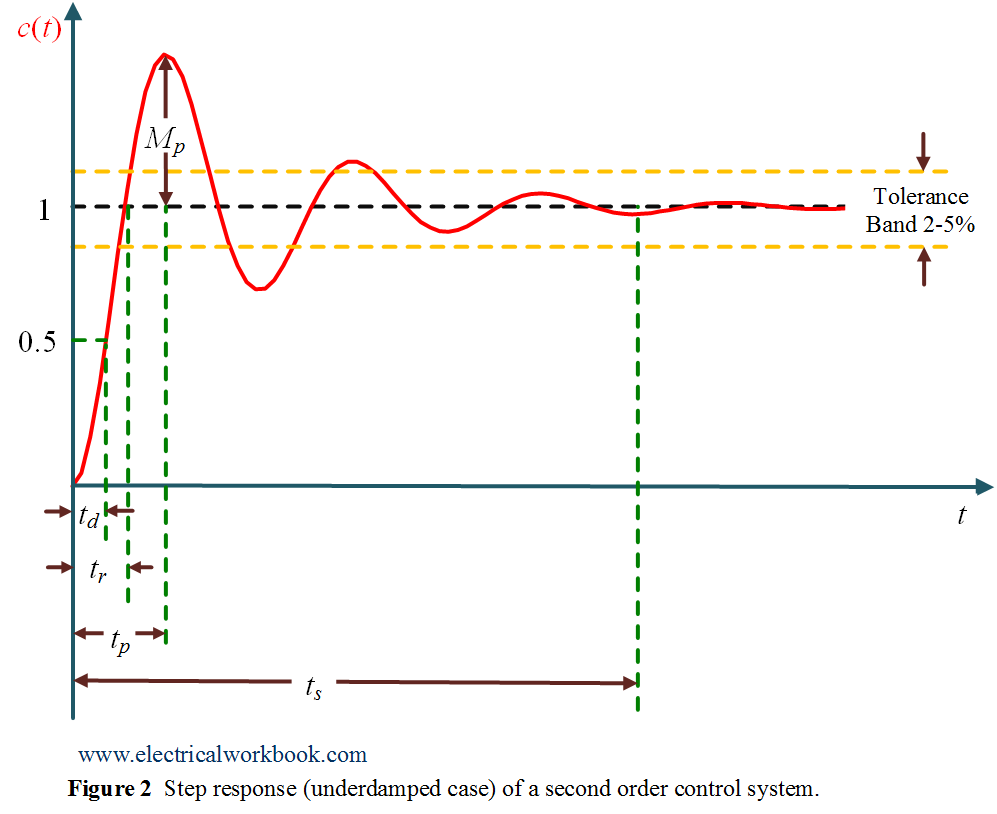
Peak time $(t_p)$
The time required for the response to reach the first peak overshoot value and it occurs at time at $t = {t_p}$, so using Equation 1, we can write
\[\frac{{dc({t_p})}}{{dt}} = 0….(2)\]
Also, Equation 1 at time $t = {t_p}$ can be written as,
\[c({t_p}) = 1 – \frac{{{e^{ – \xi {\omega _n}{t_p}}}}}{{\sqrt {1 – {\xi ^2}} }}\sin ({\omega _d}{t_p} + \theta )….(3)\]
To find first maxima, differentiating Equation 3 with respect to time (t) and equating it to zero, which gives,
\[\frac{d}{{dt}}\left[ {1 – \frac{{{e^{ – \xi {\omega _n}{t_p}}}}}{{\sqrt {1 – {\xi ^2}} }}\sin ({\omega _d}{t_p} + \theta )} \right] = 0\]
\[0 – \left[ {\frac{{{e^{ – \xi {\omega _n}{t_p}}}}}{{\sqrt {1 – {\xi ^2}} }}{\omega _d}\cos ({\omega _d}{t_p} + \theta ) – \xi {\omega _n}\frac{{{e^{ – \xi {\omega _n}{t_p}}}}}{{\sqrt {1 – {\xi ^2}} }}\sin ({\omega _d}{t_p} + \theta )} \right] = 0\]
\[{\omega _d}\cos ({\omega _d}{t_p} + \theta ) – \xi {\omega _n}\sin ({\omega _d}{t_p} + \theta ) = 0\]
\[\tan ({\omega _d}{t_p} + \theta ) = \frac{{{\omega _d}}}{{\xi {\omega _n}}}….(4)\]
Put ${\omega _d} = {\omega _n}\sqrt {1 – {\xi ^2}}$ in Equation 4 gives,
\[\tan ({\omega _d}{t_p} + \theta ) = \frac{{{\omega _n}\sqrt {1 – {\xi ^2}} }}{{\xi {\omega _n}}}\]
\[\tan ({\omega _d}{t_p} + \theta ) = \frac{{\sqrt {1 – {\xi ^2}} }}{\xi }….(5)\]
Also we know that,
\[\tan \theta = \frac{{\sqrt {1 – {\xi ^2}} }}{\xi }….(6)\]
Therefore using Equation 5 and Equation 6, we can write
\[\tan ({\omega _d}{t_p} + \theta ) = \tan \theta \]
\[{\omega _d}{t_p} = n\pi \]
or simply,
\[{t_p} = \frac{{n\pi }}{{{\omega _d}}}….(7)\]
In Equation 7, n = 1, 3, 5… use for overshoots and n = 2, 4, 6… use for undershoots.