Schering Bridge is the most popularly used bridge for measurement of unknown capacitance and dielectric loss occurring in the capacitor. The circuit diagram of the Schering bridge is shown in Fig. 1.
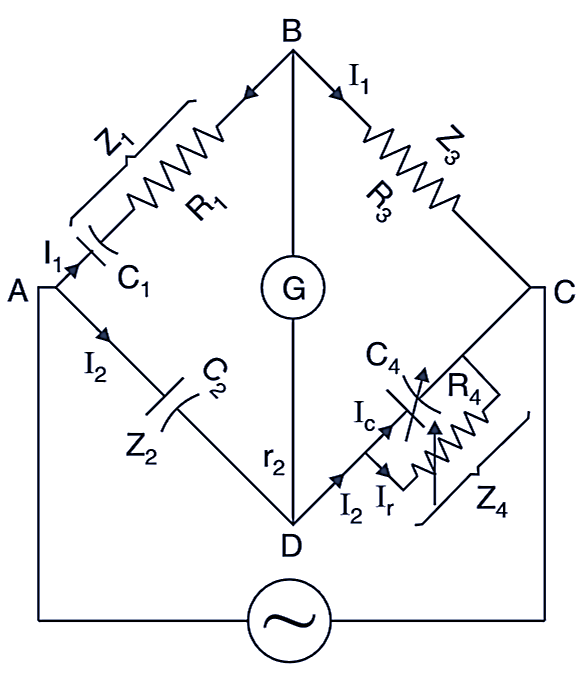
Fig. 1: Schering Bridge.
The components of the circuit are:
C1 = The unknown capacitor
R1 = A series resistance representing dielectric loss in the capacitor C1
Recall that power loss in an ideal capacitor is zero. This is the resistance contained in the capacitor, which causes power loss called dielectric loss.
R3 = a non-inductive resistor
R4 = a variable non-inductive resistor
C2 = a standard capacitor, is an air capacitor and is loss free
C4 = a variable capacitor parallel with R4
The balance is obtained by varying R3 (or R4).
At balance condition:
\[{{\text{Z}}_{\text{1}}}{{\text{Z}}_{\text{4}}}\text{ = }{{\text{Z}}_{\text{2}}}{{\text{Z}}_{\text{3}}}\]
or
\[\left[ {{\text{R}}_{\text{1}}}\text{+ }\frac{1}{\text{j}\omega {{\text{C}}_{\text{1}}}} \right]\left[ \frac{{{\text{R}}_{\text{4}}}}{\text{1+j}\omega {{\text{C}}_{\text{4}}}{{\text{R}}_{\text{4}}}} \right]\text{ = }\!\!~\!\!\text{ }\left[ \frac{1}{\text{j}\omega {{\text{C}}_{\text{2}}}} \right]{{\text{R}}_{\text{3}}}\]
or
\[\left[ {{\text{R}}_{\text{1}}}\text{+ }\frac{1}{\text{j}\omega {{\text{C}}_{\text{1}}}} \right]{{\text{R}}_{\text{4}}}\text{ = }\!\!~\!\!\text{ }\frac{{{\text{R}}_{\text{3}}}}{\text{j}\omega {{\text{C}}_{\text{2}}}}\left( \text{1+j}\omega {{\text{C}}_{\text{4}}}{{\text{R}}_{\text{4}}} \right)\]
or
\[{{\text{R}}_{\text{1}}}{{\text{R}}_{\text{4}}}\text{+ }\frac{1}{\text{j}\omega {{\text{C}}_{\text{1}}}}{{\text{R}}_{\text{4}}}\text{ = }\!\!~\!\!\text{ }\frac{{{\text{R}}_{\text{3}}}}{\text{j}\omega {{\text{C}}_{\text{2}}}}\text{+}\frac{\text{j}\omega {{\text{C}}_{\text{4}}}{{\text{R}}_{\text{4}}}{{\text{R}}_{\text{3}}}}{\text{j}\omega {{\text{C}}_{\text{2}}}}..(1)\]
Since,
\[\left( \frac{\text{1}}{\text{j}}=-\text{j} \right)\]
Thus, Equation 1 written as
\[{{\text{R}}_{\text{1}}}{{\text{R}}_{\text{4}}}-\frac{\text{j}{{\text{R}}_{\text{4}}}}{\omega {{\text{C}}_{\text{1}}}}=-\frac{\text{j}{{\text{R}}_{\text{3}}}}{\text{j}\omega {{\text{C}}_{\text{2}}}}\text{+}\frac{{{\text{C}}_{\text{4}}}{{\text{R}}_{\text{4}}}{{\text{R}}_{\text{3}}}}{{{\text{C}}_{\text{2}}}}\]
Now equating real terms
\[{{\text{R}}_{\text{1}}}{{\text{R}}_{\text{4}}}=\frac{{{\text{C}}_{\text{4}}}{{\text{R}}_{\text{4}}}{{\text{R}}_{\text{3}}}}{{{\text{C}}_{\text{2}}}}\]
or
\[{{\text{R}}_{\text{1}}}=\frac{{{\text{R}}_{\text{3}}}{{\text{C}}_{\text{4}}}}{{{\text{C}}_{\text{2}}}}\]
Equating imaginary terms
\[-\frac{\text{j}{{\text{R}}_{\text{4}}}}{\omega {{\text{C}}_{\text{1}}}}=-\frac{\text{j}{{\text{R}}_{\text{3}}}}{\omega {{\text{C}}_{\text{2}}}}\]
or
\[{{\text{C}}_{\text{1}}}=\frac{{{\text{R}}_{\text{4}}}{{\text{C}}_{\text{2}}}}{{{\text{R}}_{\text{3}}}}\]
Note:
(a) The schering bridge is particularly suitable for low capacitance measurement but time bridge is usually supplied from a high frequency/high voltage source.
(b) Thus bridge is like Wein bridge. The difference is that here is a R1C1 series circuit while in Wein bridge we use an R1L1 series circuit.